Hallo Ela,
f(x) = e-0,5*x^2 = 1/e0,5*x^2
Da x2 den gradzahligen Exponenten 2 hat, ist die Funktion achsensymmetrisch zur y-Achse:
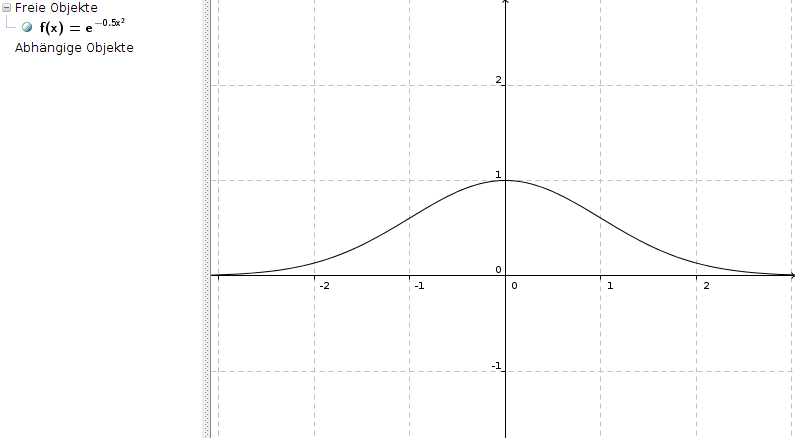
Achsenschnittpunkte
Mit der x-Achse
1/e0,5*x^2 = 0 | * e0,5*x^2
1 = 0 | unwahr, also keine Schnittpunkte mit der x-Achse
Mit der y-Achse
1/e0,5*0^2 = 1/1 = 1
Schnittpunkt mit der y-Achse = (0|1)
Extrema:
1. Ableitung (innere Ableitung * äußere Ableitung)
Innere Ableitung = -1 * x
Äußere Ableitung = e-0,5*x^2
f'(x) = -x * e-0,5*x^2
2. Ableitung (Produktregel)
(uv)' = u'v + uv'
u = -x | u' = -1
v = e-0,5*x^2 | v' = -x * e-0,5*x^2
f''(x) = - e-0,5*x^2 + x2 * e-0,5*x^2
Notwendige Voraussetzung für Extremum: f'(x) = 0
-x * e-0,5*x^2 = 0
Da e"irgendwas" stets ≠ 0, wird die 1. Ableitung nur 0 für x = 0
Hinreichende Bedingung für Extremum: f''(x) ≠ 0
f''(0) = - 1 + 0 < 0, also Maximum an der Stelle x = 0
Dies noch in die Ursprungsfunktion eingesetzt, um den y-Wert zu erhalten:
f(0) = e-0,5*0^2 = e-0 = 1/e0 = 1/1 = 1
Es gibt also ein Maximum an (0|1).
Wendepunkte:
Notwendige Bedinung für Wendepunkte: f''(x) = 0
f''(x) = - e-0,5*x^2 + x2 * e-0,5*x^2 lässt sich schreiben als
e-0,5*x^2 * (x2 - 1)
Dieser Term wird 0 nach dem oben Gesagten nur 0 für
x2 - 1 = 0
x2 = 1
x1,2 = ± 1
Nun müsste man noch überprüfen, ob f'''(1) und f'''(-1) ≠ 0 sind (hinreichende Bedingung für Wendepunkt). Das erspare ich mir jetzt, da man ja in der Grafik sieht, dass an diesen Stellen tatsächlich Wendepunkte liegen. Auch müsste man noch 1 bzw. -1 in die Ursprungsfunktion einsetzen, um die y-Koordinaten zu erhalten.
Teil b) vielleicht nachher, falls kein anderer sich erbarmt :-)
(Ist nicht bös gemeint!)
Besten Gruß