Bestimme zur Wahrscheinlichkeitsdichte ... das 75% Quantil und den Median.

Question

Kann mir eventuell einer bei dieser Frage helfen?



Bestimmen sie zu der Wahrscheinlichkeitsdichte

f(x) =         {0        ,                  für x ≤ 1

                 {(x-1)²                     für 1 ≤ x ≤ 2

                 {-3/4x + 5/2            für 2 ≤ x ≤ 10/3

                 {0                           für x ≥ 10/3

das 75% Quantil und den Median.

Als Hinweis ist gegeben, dass eine Skizze der Verteilungsfunktion bei der Berechnung der Quantile helfen kann.

Könnt ihr mir dabei helfen?

Answer 1

Zunächst sollte man überprüfen, ob f ( x ) überhaupt eine Verteilungsfunktion ist, ob also gilt:

∫_-∞^∞ f ( x )  dx = 1

Da f ( x ) stückweise definiert ist, muss auch stückweise integriert werden, also:

∫_-∞^∞ f ( x )  dx = ∫_-∞¹ f ( x )  dx + ∫₁² f ( x )  dx + ∫₂^10/3 f ( x )  dx + ∫_10/3^∞ f ( x )  dx

= 0 + ∫₁² f ( x )  dx + ∫₂^10/3 f ( x )  dx + 0

= ∫₁² ( x - 1 ) ²  dx + ∫₂^10/3 ( - 3 / 4 ) x + ( 5 / 2 ) dx

= [ ( 1 / 3 ) x ³ - x ² + x ]₁² + [ - ( 3 / 8 ) x ² + ( 5 / 2 ) x ] ₂^10/3

= [ ( 8 / 3 ) - 4 + 2 ] - [ ( 1 / 3 ) + 1 - 1 ] + [ ( - 300 / 72 )  + 50 / 6 ) ] - [ ( - 12 / 8 ) + [ 10 / 2 ) ]

= ( 2 / 3 )  -  (1 / 3 ) + ( 25  / 6 )  - ( 7 / 2 )

= ( 1 / 3 ) + ( 2 / 3 )

= 1

f ( x ) ist also eine Verteilungsfunktion.

 

Das 75 % Quantil ist diejenige Stelle b für die gilt:

∫_-∞^b f ( x )  dx = 3 / 4

Wie oben schon gezeigt wurde, ist

∫_-∞² f ( x )  dx = 1 / 3

Der Wert von b muss daher im Intervall [ 2 .. ( 10 / 3 ) ] liegen, und zwar muss gelten:

( 1 / 3 ) + ∫₂^b f ( x )  dx = 3 / 4

<=> ∫₂^b f ( x )  dx = ( 3 / 4 ) - ( 1 / 3 ) = 5 / 12

<=> ∫₂^b ( - 3 / 4 ) x + ( 5 / 2 ) dx = 5 / 12

<=> [( - 3 / 8 ) x ² + ( 5 / 2 ) x ] ₂^b = 5 / 12

<=> [ ( - 3 / 8 ) b ² + ( 5 / 2 ) b ]  - [ ( - 12 / 8 ) + 5  ] = 5 / 12

<=> ( - 3 / 8 ) b ² + ( 5 / 2 ) b + ( 12 / 8 ) - 5 - 5 / 12 = 0

<=> ( - 3 / 8 ) b ² + ( 5 / 2 ) b - ( 37 / 12 ) = 0

<=> b ² - ( 20 / 3 ) b + ( 74 / 9 ) = 0

Löst man diese quadratische Gleichung, so erhält man zwei Lösungen, von denen eine im Intervall [ 2 ... ( 10 / 3 ) ] liegt,  nämlich:

b = ( 10 / 3 )  - √ ( 2 / 3 ) ≈ 2,5168

Das 75 % - Quantil von f ( x ) ist  also b = ( 10 / 3 )  - √ ( 2 / 3 )

 

Ebenso errechnet man den Median ( 50 % - Quantil), indem man ansetzt:

∫_-∞^b f ( x )  dx = 1/ 2

Es ergibt sich:

<=> ∫₂^b f ( x )  dx = ( 1 / 2 ) - ( 1 / 3 ) = 1 / 6

...

<=> ( - 3 / 8 ) b ² + ( 5 / 2 ) b + ( 12 / 8 ) - 5 - 1 / 6 = 0

<=> ( - 3 / 8 ) b ² + ( 5 / 2 ) b - 11 / 3  = 0

Wiederum erhält man zwei Lösungen, von denen eine im Intervall [ 2 ... ( 10 / 3 ) ] liegt,  nämlich:

b = ( 10 / 3 )  - √ ( 4 / 3 ) ≈ 2,179

Der Median ( 50 % - Quantil) von f ( x ) ist  also b = ( 10 / 3 )  - √ ( 4 / 3 )

Hier ein Schaubild von f ( x ) , welches stückweise definiert ist: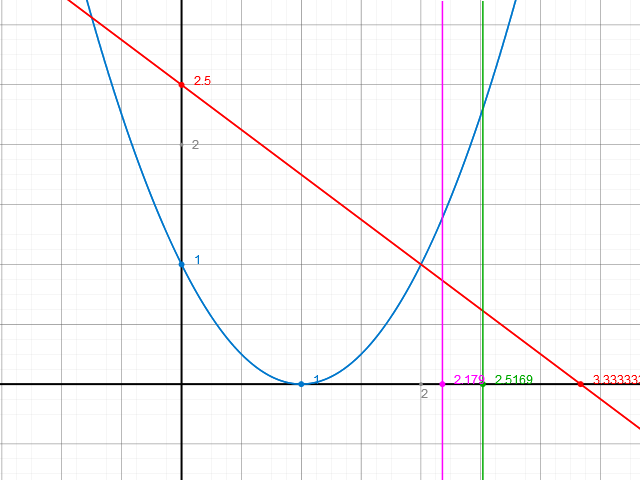

f ( x ) ist im Intervall [1 .. 2 ] durch die blaue und im Intervall [ 2 .. ( 10 / 3 ) ] durch die rote Kurve gegeben.

Eingezeichnet sind zudem das 75 % - Quantil und der Median.

Comments

Ich bin so frei und ergänze die Skizze mit einer weiteren, die die Funktionen abschnittweise zeichnet :) / Mein erster Test mit dem Desmos Plotter:

 

Link:

Unser Funktionsplotter, den JotEs benutzt hat, ist zwar gut, kann die Intervalle leider noch nicht ganz so schön.

---

Vielen Dank, Kai, so ist es natürlich viel schöner, auch wenn blau und rot nun vertauscht sind.

---

Finde deine Erklärung und ausführliche Beschreibung grandios. Schade das manche Lehrer das nicht so hin bekommen. Danke