erstmal vielen dank an die leute die mir helfen.
Ich war eine Zeitlang im Krankenhaus jetzt will ich für die Vergleichsklausur in der 11 lernen doch ich brauche die Lösungen um sicher zu gehen ob es richtig ist wäre total nett wenn ihr mir bei manchen aufgaben hilft.
Die Abbildung:
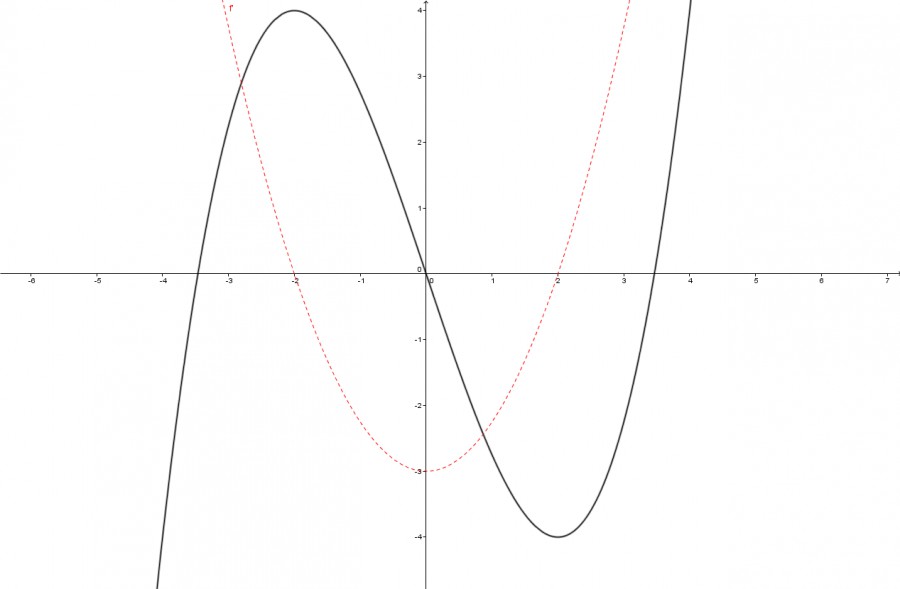
Rote ist die erste Ableitung. Schwarz die ursprungs Funktion.
Die gleichung: f(x)=0,25*x^3-3*x
Es wäre total nett wenn ihr z.b schreib aufgabe c) musst du HP und TP ausrechnen. Vielen Dank an euch nochmal
Aufgabe 1:
a) Untersuchen sie anhand der Funktionsterms, ob der Graph der Funktion symmetrisch ist.
b) Aus dem Eigenschaften des Graphen der Funktion f ergeben sich Eigenschaften des Graphen der Funktion f '
Geben siedafür zwei Bespiele an. Beziehen sie sich dabei konkret auf Eigenschaften der beiden Graphen in der Abbildung.
c) (1) Weisen sie rechnerisch nach, dass der Graph von f in H (-2I4) einen lokalen Hochpunkt und in T (2I-4) einen lokalen Tiefpunkt hat.
(2) Zecihnen Sie in die Abbildung die Gerade g ein, die durch die beiden lokalen Extrempunkte des Graphen der Funktion f verläuft, und bestimmen Sie rechnerisch die Gliechung dieser Geraden. [Kontrolle]: g:y=-2*x]
d) Der Graph der Funktion f hat in zwei Punkten P1 und P2 Tangenten, die parallel zur Geraden g aus Teilaufgabe c) verlaufen.
(1) Bestimmen sie die Punkte P1 und P2 zeichnerisch unter Verwendung des Graphen der Funktion f ' aus der Abbildung.
(2) Bestimmen sie durch eine Rechnung die genauen x-Koordinaten der Punkte P1 und P2.
e) (1) Der Graph von f wird parallel zu den Koordinatenachsen so verschoben, dass der verschobene Graph seinen lokalen Hochpunkt im Ursprung hat. Die Funktion, die zu dem verschobenen Graphen gehört, wird mir f1 bezeichnet. Geben sie eine Funktionsgleichung von f1 an.
[Hinweis: Hier in e) (1) sind keine Rechnungen erforderlich.]
(2) Nun wird die Gerade g in genau derselben Weise wie der Graph von f verschoben. Die verschobene Gerade wird mit g1 bezeichnet. Begründen Sie, dass sie Geraden g un g1 identisch sind.