Zunächst solltest du eine Skizze der Graphen der Funktionen anfertigen. Die sieht etwa so aus:
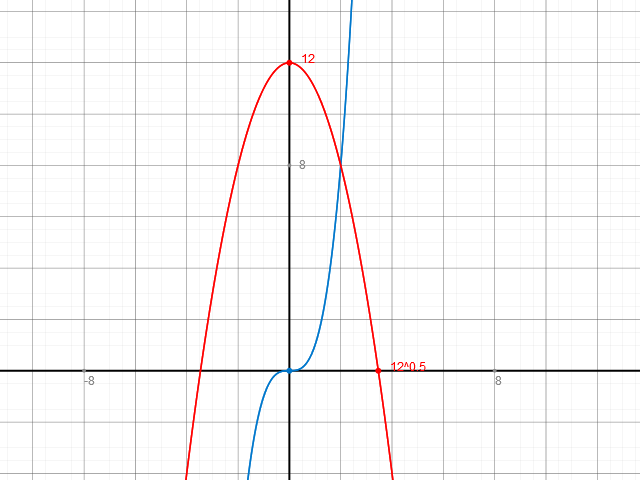
An dem Schaubild kannst du erkennen, von wo und insbesondere, BIS wo du integrieren musst, nämlich von 0 bis zu der x-Koordinate xs des Schnittpunktes von f und g. Diese x-Koordinate muss du zunächst berechnen. Dazu setzt du die Funktionsterme gleich:
x 3 = - x 2 + 12
<=> x 3 + x 2 - 12 = 0
Nun musst du eine Nullstelle raten. Dazu empfiehlt es sich, die positiven und negativen Teiler des absoluten Gliedes ( also der 12 ) auszuprobieren, denn wenn eine Polynomfunktion eine ganzzahlige Nullstelle hat, dann ist sie Teiler des absoluten Gliedes. (Im Übrigen kann man schon am Graphen vermuten, dass x = 2 die x-Koordinate des Schnittpunktes von f und g und somit Nullstelle von f - g sein könnte.)
Um nun die Flächenmaßzahl der bezeichneten Fläche zu bestimmen, muss also das Integral von 0 bis 2 über g - f bestimmt werden, also:
A = ∫02 g - f dx
= ∫02 - x 2 +12 - x 3 dx
= ∫02 - x 3 - x 2 +12 dx
= [ - ( 1 / 4 ) x 4 - ( 1 / 3 ) x 3 + 12 x ]02
= [ - 4 - ( 8 / 3 ) + 24 ] - [ 0 ]
= 17,333