Fertige zunächst ein Schaubild der Graphen von f ( x ) und g ( x ) an, damit du siehst, um welche Flächen es überhaupt geht:
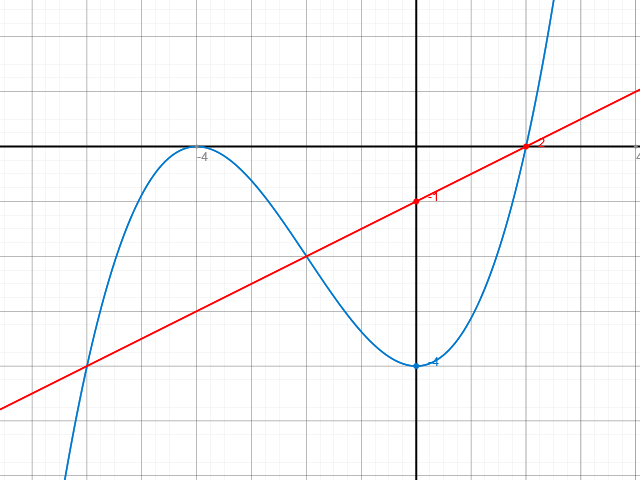
Der Graph von f ( x ) ist blau, der von g ( x ) rot eingezeichnet. Man erkennt deutlich, welche Flächen gemeint sind.
Bestimme nun die Schnittpunkte von f ( x ) und g ( x ) durch Gleichsetzen ihrer Funktionsterme und Auflösen nach x:
Durch "scharfes Hinsehen" erkennt man, dass der Funktionsterm von g ( x ) den Faktor ( x - 2 ) enthält. Diesen erhält man explizit, indem man den Faktor 1 / 2 ausklammert, also:
g ( x ) = ( 1 / 2 ) ( x - 2 )
Nun Gleichsetzen:
$$\frac { 1 }{ 8 } { \left( x+4 \right) }^{ 2 }\left( x-2 \right) =\frac { 1 }{ 2 } \left( x-2 \right)$$
Diese Gleichung ist offensichtlich wahr, wenn der Faktor x - 2 den Wert 0 annimmt, wenn also gilt:
x = 2
Für x ≠ 2 darf man durch ( x - 2 ) dividieren und erhält :
$$\frac { 1 }{ 8 } { \left( x+4 \right) }^{ 2 }\left( x-2 \right) =\frac { 1 }{ 2 } \left( x-2 \right)$$$$\frac { 1 }{ 8 } { \left( x+4 \right) }^{ 2 }=\frac { 1 }{ 2 }$$$$\Leftrightarrow { \left( x+4 \right) }^{ 2 }=4$$$$\Leftrightarrow x+4=\pm 2$$$$\Leftrightarrow { x=-2-4\vee }x=2-4$$$$\Leftrightarrow { x=-6\vee }x=-2$$
Die drei Schnittpunkte f ( x ) und g ( x ) liegen also bei
x = - 6
x = - 2
x = 2
Um nun zu zeigen, dass die beiden Flächeninhalte gleich sind, muss man die Gleichheit der Beträge der Integrale über die Differenzen von f und g zeigen, zum Einen im Intervall - 6 bis -2 und zum Anderen im Intervall - 2 bis 2.
Man muss also zeigen:
$$\left| \int _{ -6 }^{ -2 }{ f(x)-g(x)dx } \right| =\left| \int _{ -2 }^{ 2 }{ f(x)-g(x)dx } \right|$$$$\Leftrightarrow \left| \int _{ -6 }^{ -2 }{ \frac { 1 }{ 8 } { x }^{ 3 }+\frac { 3 }{ 4 } { x }^{ 2 }-\frac { 1 }{ 2 } { x }-3 dx } \right| =\left| \int _{ -2 }^{ 2 }{ \frac { 1 }{ 8 } { x }^{ 3 }+\frac { 3 }{ 4 } { x }^{ 2 }-\frac { 1 }{ 2 } { x }-3 dx } \right|$$$$\Leftrightarrow \left| { \left[ \frac { 1 }{ 32 } { x }^{ 4 }+\frac { 1 }{ 4 } { x }^{ 3 }-\frac { 1 }{ 4 } { { x }^{ 2 } }-3x \right] }_{ -6 }^{ -2 } \right| =\left| { \left[ \frac { 1 }{ 32 } { x }^{ 4 }+\frac { 1 }{ 4 } { x }^{ 3 }-\frac { 1 }{ 4 } { { x }^{ 2 } }-3x \right] }_{ -2 }^{ 2 } \right|$$$$\Leftrightarrow \left| \left( \frac { 1 }{ 2 } -2-1+6 \right) -\left( \frac { 81 }{ 2 } -54-9+18 \right) \right| =\left| \left( \frac { 1 }{ 2 } +2-1-6 \right) -\left( \frac { 1 }{ 2 } -2-1+6 \right) \right|$$$$\Leftrightarrow \left| 3,5-(-4,5) \right| =\left| -4,5-3,5 \right|$$$$\Leftrightarrow \left| 8 \right| =\left| -8 \right|$$$$\Leftrightarrow 8=8$$
Damit ist die Gleichheit gezeigt und auch der Wert des Flächeninhaltes berechnet.
Etwas einfacher und ohne Integral ist die Gleichheit zu zeigen, wenn man die Symmetrie ausnutzt. Beide Graphen scheinen punktsymmetrisch zum Punkt ( - 2 | - 2 ) zu sein. Zum Nachweis, dass dies der Fall ist, verschiebt man beide Graphen so, dass dieser Punkt im Ursprung zu liegen kommt, also:
f*( x ) = f ( x - 2 ) + 2 = ( 1 / 8 ) ( x - 2 + 4 ) 2 ( x - 2 - 2 ) + 2 = ( 1 / 8 ) ( x + 2 ) 2 ( x - 4 ) + 2
g* ( x ) = g ( x - 2 ) + 2 = ( 1 / 2 ) ( x - 2 ) -1 + 2 = ( 1 / 2 ) x
Diese sehen dann so aus:
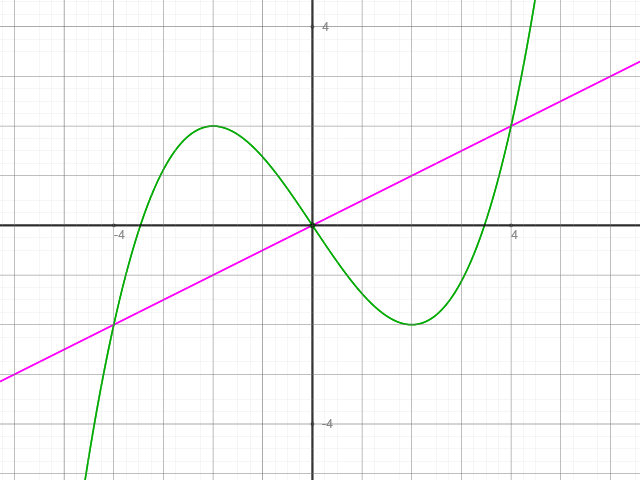
Nun zeigt man die Symmetrie dieser verschobenen Funktionen zum Ursprung, dass also gilt:
f * ( x ) = - f * ( x )
sowie:.
g * ( x ) = - g * ( - x )
Wenn beide Funktionen symmetrisch zum Ursprung sind, dann müssen auch die beiden von ihnen eingeschlossenen Flächen gleich groß sein.
Also:
$${ f }^{ * }(x)={ -f }^{ * }(-x)$$$$\Leftrightarrow \frac { 1 }{ 8 } (x+2)^{ 2 }(x-4)+2=-\left( \frac { 1 }{ 8 } (-x+2)^{ 2 }(-x-4)+2 \right)$$$$\Leftrightarrow (x+2)^{ 2 }(x-4)+16=-(-x+2)^{ 2 }(-x-4)-16$$$$\Leftrightarrow ({ x }^{ 2 }+4x+4)(x-4)+32=({ x }^{ 2 }-4x+4)(x+4)$$$$\Leftrightarrow { x }^{ 3 }-4{ x }^{ 2 }+4{ x }^{ 2 }-16x+4x-16+32={ x }^{ 3 }-4{ x }^{ 2 }+4{ x }^{ 2 }-16x+4x+16$$$$\Leftrightarrow 0=0$$
sowie
$${ g }^{ * }(x)={ -g }^{ * }(-x)$$$$\Leftrightarrow \frac { 1 }{ 2 } x=-\frac { 1 }{ 2 } (-x)$$$$\Leftrightarrow 0=0$$
Beide Funktionen sind also symmetrisch zum Ursprung und damit sind auch die von ihnen eingeschlossenen Flächen gleich groß.