Lineare Ungleichungen

Question

Löse das Gleichungssystem grafisch. Gehört die Randgerade mit zur Lösungsmenge, so zeichne sie ,, durchgezogen" , wenn nicht, dann zeichne sie gestrichelt. a) y 3 b) y-2> x y+3x> 5

Comments

a) y 3 b) y-2> x y+3x> 5 .

---

Mit

a) y 3

kann ich leider nichts anfangen. Was soll das bedeuten?

---

Mein Handy spinnt ein bisschen. Das soll heißen : a) y kleiner gleich 1 || 2x-3y größer gleich 3 b) y-2 größer gleich x || y+3x größer gleich 5

Answer 1

OK, also dann:

a)

Löse die Ungleichungen nach y auf und schreibe sie dann zunächst als Gleichungen:

y ≤ 1 -> y = 1

2 x - 3 y ≥ 3

<=> 3 y ≤ 2 x - 3

<=> y ≤ ( 2 / 3 ) x - 1

-> y = ( 2 / 3 ) x - 1
 

Durch

y = 1

<=> y = 0 x + 1

wird eine Gerade beschrieben, die parallel zur x-Achse (Steigung 0) durch den Punkt ( 0 | 1 )  verläuft. Wegen y ≤ 1 gehören zur Lösungsmenge alle Punkte der x-y-Ebene, die unterhalb oder auf dieser Geraden liegen, also:

L₁ = { ( x | y ) | y ≤ 1 }

Die zweite Gleichung

<=> y = ( 2 / 3 ) x - 1 

beschreibt eine Gerade mit der Steigung 2 / 3 , die durch den Punkt ( 0 | - 1 ) verläuft.

y ≤ ( 2 / 3 ) x - 1

gehören zur Lösungsmenge alle Punkte der x-y-Ebene, die unterhalb oder auf dieser Geraden liegen, also:

L₂ = { ( x | y ) | y ≤ ( 2 / 3 ) x - 1 }

Graphisch sieht das so aus:

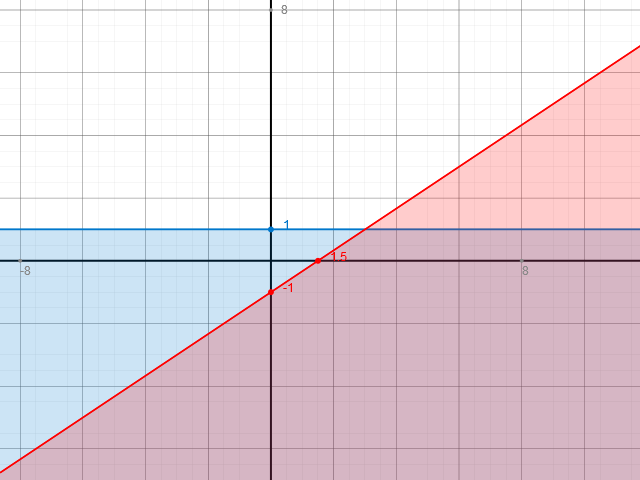
Der blaue Bereich stellt die Lösungsmenge L₁ und der rote Bereich die Lösungsmenge L₂ dar.

Die Lösungsmenge L des Ungleichungssystems ist nun die Schnittmenge von L₁ und L₂, dargestellt durch den blau-roten Bereich. Die Ränder dieses Bereichs gehören wegen der kleiner-gleich-Zeichen mit zur Lösungsmenge.

 

b)

Hier sieht die Grafik so aus:

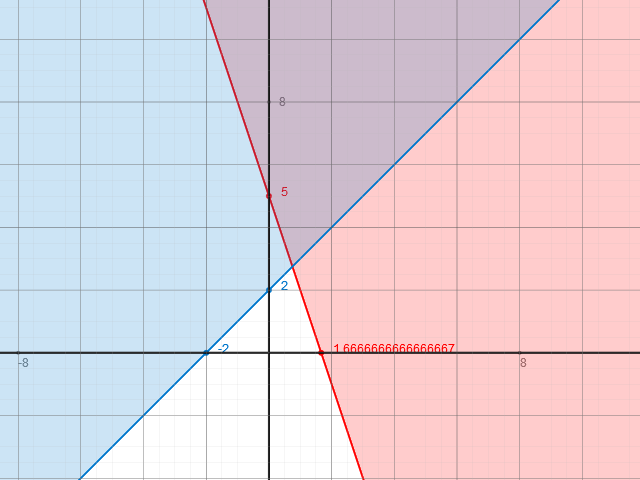
Der blaue Bereich stellt wieder die Lösungsmenge L₁ und der rote Bereich die Lösungsmenge L₂ dar.

Die Lösungsmenge L des Ungleichungssystems ist wieder die Schnittmenge von L₁ und L₂, dargestellt durch den blau-roten Bereich. Die Ränder dieses Bereichs gehören wegen der echt-größer-Zeichen nicht mit zur Lösungsmenge, müssen also gestrichelt gezeichnet werden.