Verfahren für Gleichungssysteme

Question

1)Grafische Lösungsverfahren!

2)Einsetzungsverfahren!

3)Gleichsetzungsverfahren!

4)Additionsverfahren!

Comments

Wo liegt dein Problem ?

Answer 1

Hi,

Gleichsetzungsverfahren

|. 4=5x+y

||. 6=8x+2y

Du stellst jetzt beide Gleichungen so um, dass y auf einer Seite steht und der Rest auf einer Seite, also:

|. 4=5x+y |-5x

   4-5x=y

||. 6=8x+2y |-8x

    6-8x=2y |:2

    3-4x=y

 

Jetzt kannst Du beide Gleichungen gleich setzen, also:

4-5x=3-4x |+4x

4-x=3 |-4

-x= -1 |*(-1)

 x=1

x in eine der beiden Gleichungen einsetzen um y zu haben.

y= 4-5*1= -1

 

Einsetzungsverfahren

|.4=5x+y

||.6=8x+2y

Du stellst jetzt eine Gleichung nach x oder nach y auf. Das kannst Du dir aussuchen. Ich stelle jetzt einfach mal nach y um.

4=5x+y |-5x

y= (4-5x)

Jetzt kannst Du diese Gleichung in die 2. Gleichun für y einsetzen, deshalb heißt es auch Einsetzungsverfahren

6=8x+2*(4-5x) |Ausmultiplizieren (Distrubutivgesetz)

6=8x+8-10x

6=8-2x |-8

-2=-2x |:2

x=1

x wie immer in diese Gleichung einsetzen y= 4-5x = y= 4-5*1= -1

 

Additionsverfahren

|. 4=5x+y |*(-2)

||.6=8x+2y

_____________

|. -8=-10x-2y

||. 6=8x+2y

|+||

-2=-2x |:(-2)

x= 1

x in eine eine der beiden Gleichungen einsetzen um y raus zu bekommen, aber hier musst du erstmal eine Gleichung nach y umstellen: 

4=5x+y |-5x

y= 4-5x

y=4-5*1

y= -1

 

Du siehst bei allen kommt das selbe raus.

Grafisches Lösen

Du kennst bestimmt diese Form einer Geradengleichung: y=mx+b

b= y-Achsenabschnitt

m= Steigung

| 4=5x+y

|| 6=8x+2y

Erstmal musst Du alle beide Gleichungen in diese Form bringen:

|. 4=5x+y |-5x

   4-5x=y

||. 6=8x+2y |-8x |:2

    3-4x=y

 

Jetzt kannst Du diese beiden Gleichungen in ein Koordinatensystem zeichen:

 

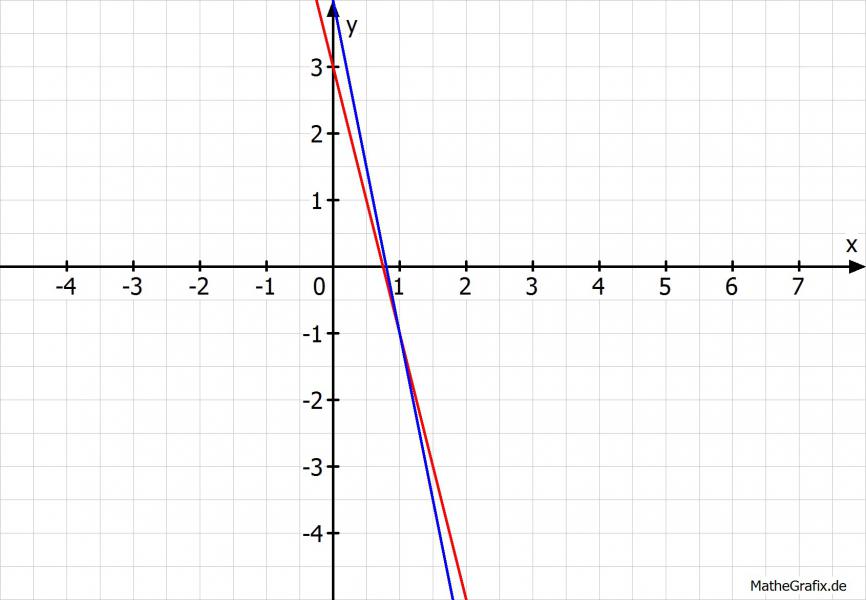
Der Schnittpunkt dieser beiden Funktionen ist dann die Lösung. Du siehst der Schnittpunkt ist bei S(1|-1)

Und genau das hatten wir auch immer raus :)

 

Ich hoffe das war jetzt verständlich :)

 

Liebe Grüße

Comments

nur eine Bemerkung zur zeichnerischen Lösung. Du schreibst "Du siehst der Schnittpunkt ist bei S(1|-1)". Dass man dies in einer solchen Zeichnung, besonders wenn sie von Hand gezeichnet (und möglicherweise nicht besonders präzise) ist, wirklich sieht, ist eher unwahrscheinlich. Schau dir die Zeichnung einfach noch einmal an und frag' dich: "Wo genau ist der Schnittpunkt?".  Da (bei gleichen Skaleneinheiten auf der x-Achse und der y-Achse) der Winkel zwischen den beiden Geraden sehr klein ist, handelt es sich um einen sogenannten "schleifenden Schnittpunkt", dessen genaue Position optisch nur sehr ungenau festgelegt werden kann. Man könnte dieses Problem zwar zeichnerisch teilweise beheben, indem man eine neue Zeichnung der Umgebung des vermuteten Schnittpunktes ("Zoom") erstellen würde, mit anderen Skalierungen der Achsen.

Prinzipiell sind derartige Beispiele aber vermutlich dazu gedacht, den Gedanken "Rechnen ist genauer als Zeichnen" zu transportieren. Als Argument dafür, auf zeichnerische Lösungen grundsätzlich zu verzichten, muss ich dies aber weit von mir weisen ! ich bin ein vehementer Befürworter geometrischer und anschaulicher Argumentationen in vielen Bereichen der Mathematik (eigentlich überall da, wo es überhaupt geht) und folglich auch in der Schulmathematik.

LG ,    Yakob

---

ja Du hast naürlich Recht. Danke.

---

Womm, starke Antwort Emre!

---

Man sieht ungefähr einen Schnittpunkt bei S(1|-1). Man könnte dann noch recht leicht begründen das das tatsächlich der Schnittpunkt ist. Das geschieht recht einfach durch einsetzen.

Wenn man für die Zeichnung eventuell eine Wertetabelle gemacht hat, weiss man eh das an dieser Stelle tatsächlich auch die Funktionswerte gleich sind.

Aber man bekommt halt Schwierigkeiten wenn der Schnittpunkt nicht so schön sich ganzzahlig darstellen lässt.

Übrigens auch von mir ein ganz dickes Lob an Emre. Die Antwort hast du wirklich sehr schön gemacht !

---

ja da hat der Mathecoach recht :)

wow ein dickes Lob von Mathecoach zu bekommen....das bedeutet mir vieeeeel. Danke Mathecoach!!!!

Answer 2

Für die verfahren schau die Filme  bei Matheretter an , da sind die Rechenwege gut erklärt.

Answer 3

Hi,

Kannst auch mal hier rein schauen:

https://www.mathelounge.de/46100/artikel-lineares-gleichungssystem-additionsverfahren-erklart

Dort findest Du auch die Links zum Gleichsetzungs- und Einsetzverfahren :).


Grüße