Zu a)
Skizze:
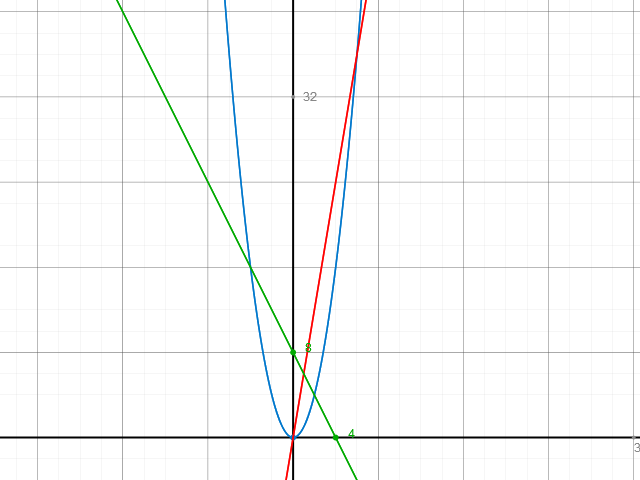
f ( x ) = x 2
g ( x ) = 6x
h ( x ) = - 2 x + 8
Die drei Graphen schließen im ersten Quadranten zwei Flächen ein. Die Vereinigung dieser beiden Flächen ergibt die Fläche, die von den Graphen zu f ( x ) und g ( x ) eingeschlossen wird. Die Schnittpunkte dieser beiden Graphen haben die x-Koordinaten 0 bzw. 6.
Der Flächeninhalt A dieser Fläche ist (und somit der gesuchte Flächeninhalt) ist also:
$$A=\int _{ 0 }^{ 6 }{ 6x-{ x }^{ 2 }dx } ={ \left[ 3{ x }^{ 2 }-\frac { 1 }{ 3 } { x }^{ 3 } \right] }_{ 0 }^{ 6 }$$$$=(108-\frac { 216 }{ 3 } )-(0-0)=\frac { 108 }{ 3 }$$$$=36$$
Das Ergebnis stimmt mit deinem überein.
zu b)
Skizze:
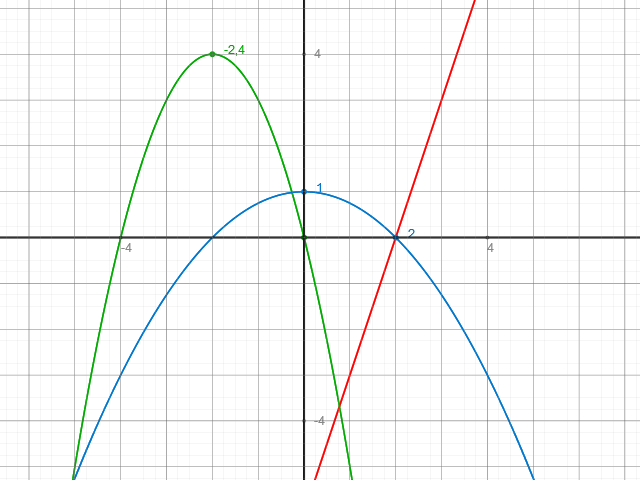
f ( x ) = 1 - ( 1 / 4 ) x 2
g ( x ) = - x 2 - 4 x
h ( x ) = 3 x - 6
Die von den drei Graphen eingeschlossene, auf den ersten Quadranten beschränkte Fläche ist gleich der Fläche, die der Graph von f ( x ) mit der x-Achse im ersten Quadranten einschließt. Der Flächeninhalt A dieser Fläche ist:
$$A=\int _{ 0 }^{ 2 }{ 1-(1/4){ x }^{ 2 }dx } ={ \left[ x-\frac { 1 }{ 12 } { x }^{ 3 } \right] }_{ 0 }^{ 2 }$$$$=(2-\frac { 2 }{ 3 } )-(0-0)$$$$=\frac { 4 }{ 3 }$$
Hier stimmt mein Ergebnis nicht mit deinem überein.
zu c)
Skizze:
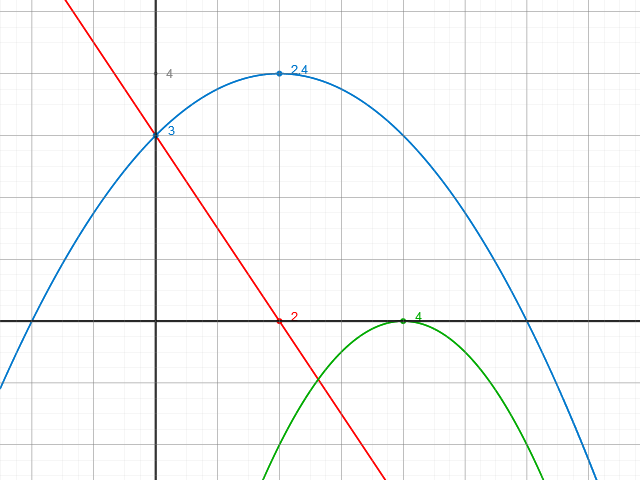
f ( x ) = - 0.25 x 2 + x + 3
g ( x ) = - 0.5 ( x - 4 ) 2
h ( x ) = - 1.5 x + 3
Der gesuchte Flächeninhalt A ist hier:
$$A=\int _{ 0 }^{ 2 }{ f(x)-h(x)dx+\int _{ 2 }^{ 6 }{ f(x)dx } }$$$$=\int _{ 0 }^{ 2 }{ -\frac { 1 }{ 4 } { x }^{ 2 }+x+3+\frac { 3 }{ 2 } x-3dx+\int _{ 2 }^{ 6 }{ -\frac { 1 }{ 4 } { x }^{ 2 }+x+3dx } }$$$$=\int _{ 0 }^{ 2 }{ -\frac { 1 }{ 4 } x^{ 2 }+\frac { 5 }{ 2 } xdx+\int _{ 2 }^{ 6 }{ -\frac { 1 }{ 4 } { x }^{ 2 }+x+3dx } }$$$$={ \left[ -\frac { 1 }{ 12 } { x }^{ 3 }+\frac { 5 }{ 4 } { x }^{ 2 } \right] }_{ 0 }^{ 2 }{ +\left[ -\frac { 1 }{ 12 } { x }^{ 3 }+\frac { 1 }{ 2 } { x }^{ 2 }+3x \right] }_{ 2 }^{ 6 }$$$$=(-\frac { 8 }{ 12 } +5)-(0-0)+(-\frac { 216 }{ 12 } +18+18)-(-\frac { 8 }{ 12 } +2+6)$$$$=\frac { 52 }{ 12 } -0+18-\frac { 88 }{ 12 }$$$$=\frac { 180 }{ 12 }$$$$=15$$
Auch hier stimmt mein Ergebnis nicht mit deinem überein.