Zuerst mal die Pferdekoppel von oben. Die Seitenlängen des Rechtecks sind unbekannt; deshalb x und y. Zu erwartende Einheit von x und y ist m.
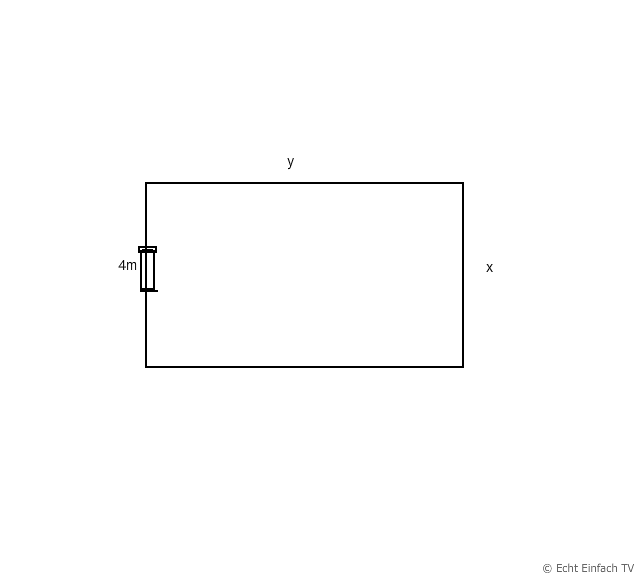
Ich nehme das erst mal genau, was im Text steht und optimiere da nichts:
Es gilt für die Fläche:
1. x*y = 640.
und für den Zaun:
2. 2x - 4 + 2y = 100.
Einige Umformungen:
2.' 2y = 104 - 2x
2.'' y = 52 - x
2.'' in 1. einsetzen:
3. x * (52-x) = 640.
52x - x^2 = 640.
4. 0= x^2 - 52x + 640
Das ist eine quadratische Gleichung. Es gilt:
x1,2 = (52-±√ ( 52^2 - 4*640) ) /2
x1,2 = (52-±√ 144 ) /2
x1,2 = (52-±12 ) /2
x1 = 32 ; x2 = 20
In 2.'' einsetzen
y1=52-32 = 20, y2=52-20 = 32
Also: Mit x = 20 Meter und y = 32 Meter und mit x = 32 Meter und mit y = 20 Meter werden die Vorgaben genau erreicht.
Die gestellte Aufgabe ist hier eigentlich fertig gelöst.
Jetzt zur Optimierung:
Die Frage ist, das da zu oprimieren wäre; es soll ja offenbar eine Optimierungsaufgabe sein. Ich nehme an, dass er mit dem Zaun eine möglichst grosse Fläche (mehr als 640 m2 einzäunen will.
und ersetze in 3. die Fläche durch eine Funktion P(x):
3. ist neu: P(x) = x * (52- x) = 52 x - x2
Das ist eine quadratische Funktion. Ihr Graph ist eine nach unten geöffnete Parabel. Deren Scheitelpunkt ist ein sog. Hochpunkt der Funktion. Die Nullstellen sind x1= 0 und x2 = 52. Aus Symmetriegründen ist der x-Wert des Scheitelpunktes genau in der Mitte; also bei x = 26.
Dazu kann man y = 52-x berechnen. Das ist auch 26.
Die Fläche, die den Pferden zur Verfügung steht ist somit sogar. (26 m)2 = 676 m2
Probe P(26) = 52 * 26 - 262 = 676.
Optimal im Sinne der beschriebenen interpretation steckt er ein 26m * 26m grosses Flächenstück ab. Die 4m breite Lücke kann überall angebracht werden.
Zurück zur ursprünglichen Aufgabe:
Auch
4. 0= x^2 - 52x + 640
Kann mit Hilfe einer quadratischen Funktion gelöst werden.
Man muss da die Nullstellen von
f(x)= x^2 - 52x + 640
bestimmen. Und bekommt sie z.B. durch Faktorisierung:
f(x) = (x -32 )(x-20) -> x1=32 und x2=20, von da an weiter wie zuerst.
Bei der Faktorisierung benutzt man
(x+a)(x+b) = x2 + (a+b)x + ab