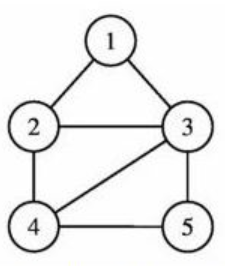
Erstelle eine boolsche Formel, die genau dann erfült ist, wenn der obige Graph mit drei Faben so eingefärbt werden kann, dass angrenzende Knoten nicht die selbe Farbe haben. Benutze die Variablen ai, bi, ci für \( i \in\{1, \ldots, 5\} \) zum repräsentieren der Färbung eines Knotens. Die Variable ai bzw. bi bzw. ci gilt genau dann, wenn der Knoten i mit Farbe a bzw. b bzw. c gefärbt ist. Jedem Knoten muss genau eine Farbe zugewiesen werden.
Hinweis: Die Abgabe hat die Form: !a1 & b1 | c1
Ansatz:
Die ist die Aufgabe die ich lösen muss. Da ich von Logik keine Ahnung hab und das noch wirklich gemacht hab ... es aber leider in den Übungen dran kam jedoch nicht wirklich ausgibig behnadelt wurde suche ich nun hier Hilfe.
Ich hatte als Vorschlag a1&b2|c3 & b2&a1|c3|a4 & c3&a1|b2|a4|b5 & b5&c3|a4
scheint aber wohl ziemlich falsch zu sein.
Naja vielleicht wisst ihr mehr darüber?