Hallöle :-)
1.) Gegeben sei das Dreieck ABC A(-1/-2) B(4/-1) C(1,5/3)
a) Stellen Sie das Dreieck in einen Koordinatensystem graphisch dar.
Kein Problem:
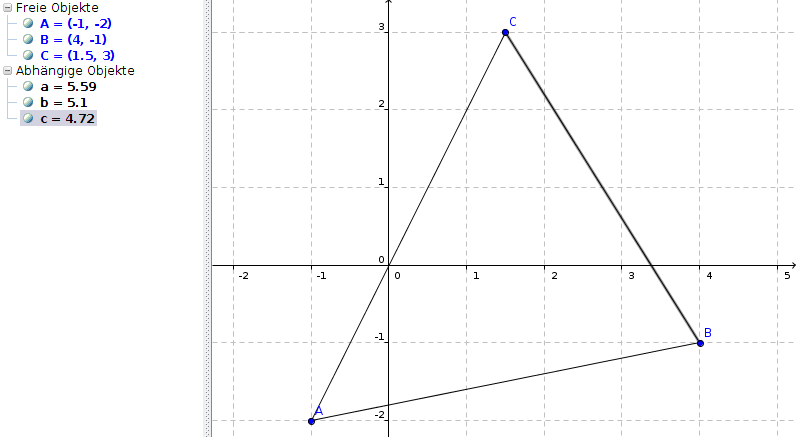
b) geben Sie die Funktion an, die die drei Dreiecksseiten als Graph haben.
Es sind offensichtlich lineare Funktionen - man kann sie mit einem Lineal zeichnen :-)
Wenn wir nicht auf Vektorrechnung zurückgreifen wollen, bedienen wir uns der allgemeinen Form einer linearen Funktion:
f(x) = mx + b
Für die Gerade, auf der AB liegt, gilt also
f(-1) = -2 = m*(-1) + b | und
f(4) = -1 = m * (4) + b
also
I. -m + b = -2
II. 4m + b = -1
II - I ergibt
5m = 1
m = 1/5
Eingesetzt in zum Beispiel I
-1/5 + b = -2
b = -2 + 1/5
b = - 9/5
Die Funktion, die die Strecke AB beinhaltet, lautet also
f(x) = 1/5 * x - 9/5
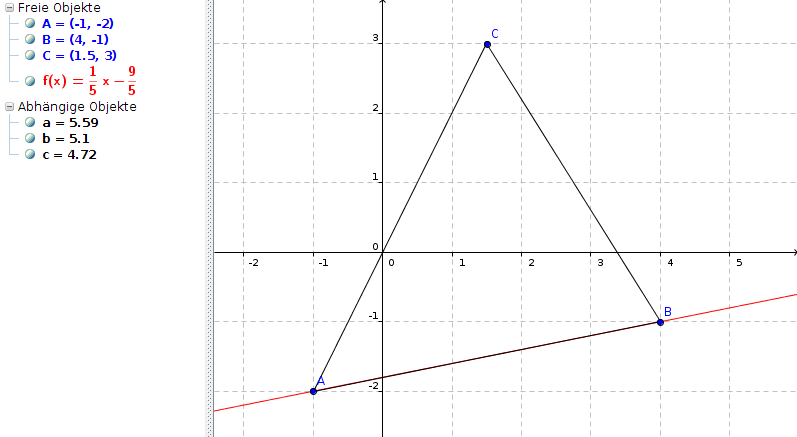
Mit den drei anderen Seiten verfährt man dann genauso :-)
c) Bestimmen Sie die Koordinaten der Seitenmittelpunkte.
Ganz einfach:
Man addiert die Koordinaten der gegebenen Punkte und dividiert sie durch 2. Zum Beispiel:
Du bist 1,60m groß, ich 1,83m. Genau auf der Hälfte liegt der Punkt
(1,60 + 1,83)/2 = 1,715
Der Seitenmittelpunkt von AB liegt also bei [(-1|-2) + (4|-1)] / 2 = (3|-3) / 2 = (1,5|-1,5)
Ist auch aus der Graphik oben recht gut abzulesen.
Seitenmittelpunkte der anderen Strecken analog - eine schöne Aufgabe für Dich :-)
d) Geben sie eine Formel an, mit deren Hilfe sie allgemein die Koordinaten des Mittelpunkts einer Strecke A(a/b) und B (c /d) berechnen können.
Das wurde quasi schon in Teilaufgabe c) beantwortet:
Addition der Koordinaten und dann Division durch 2.
Also
Der Mittelpunkt der Strecke A(a|b) und B(c|d) ist:
(a+c|b+d)/2 =
[(a+c)/2|(b+d)/2]
To be continued :-D
Liebe Grüße
Andreas