es geht um folgende Ungleichung: 2-x < 1/2 * x + 1/2
Zu dieser Aufgabe habe ich die richtige Zeichnung im Heft. Ich nehme diese Aufgaben jedoch gerne als Übung. Aber ich komme leider nicht auf das richtige Ergebnis. Habe den Term 2-x auch bereits online eingegeben, um den Graphen so nochmals zeichnerisch zu erhalten.
Nun ja, im Folgenden meine Lösung und die Zeichnung aus meinem Mathebuch.
Ich habe grundlegend immer wieder Probleme bei den Zeichnungen. Gibt es denn da nicht irgendwelche Grundregeln, die zu beachten sind? Ich meine eigentlich funktioniert in Mathe alles nach gewissen Abläufen. Aber hinsichtlich der Steigung erkennen ich das einfach nicht.
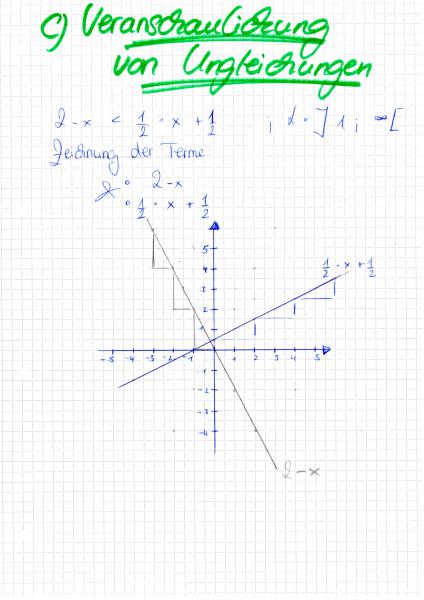
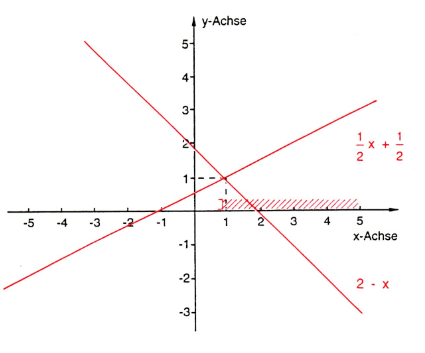
Der Unterschied ist deutlich - ein 1cm.
Mir stellt sich grundlegend die Frage, woher ich zum Beispiel auch weiß, wie der Graph verläuft. Spielen die Rechenzeichen hierbei eine Rolle? Ich habe hier den Graphen 2-x negativ verlaufen lassen, da im Term ein Minus steht. Der Term 1/2 *x + 1/2 verläuft meiner Meinung nach positiv, da dieser Term ein Plus beinhaltet.
Ich weiß, dass die Grundform m * x + n oder m * x + t heißt.
Dabei ist m die Steigung, x ist die Variable und n bzw. t ist der Punkt der y-Achse, der angibt, ob und wie weit der Graph nach oben oder unten verschoben wird. Das heißt in dieser Aufgabe beispielsweise bei 1/2 * x + 1/2, dass mir das hintere 1/2 angibt, dass ich bei 1/2 anfange das Steigungsdreieck zu zählen und der Graph durch diesen Punkt geht.
Aber wieso komme ich bei 2-x nicht auf das gleiche Ergebnis?
Ich habe auch gleich meinen persönlichen Verlauf - durch die Steigungsdreiecke - eingezeichnet.
Ich hoffe mir kann jemand helfen.