Ferner definieren wir folgende Teilmengen der Knoten bzw. Kanten von \( G: \)
\( U_{1}:=\{4,5\}, \quad U_{2}:=\{3,4,5,6\} \)
\( F_{1}:=\{(2,8),(3,5),(4,6),(1,7)\}, F_{2}:=\{(1,2),(2,8),(8,7),(7,5),(2,4)\} \)
Zeichnen Sie \( \left.G-U_{1}, C-F_{1}, G \mid U_{2}\right], C\left[F_{2}\left|,\left(G-U_{1}\right) \cap\left(C-F_{1}\right), G\right| U_{2}\right] \cup G\left[F_{2}\right\} \)
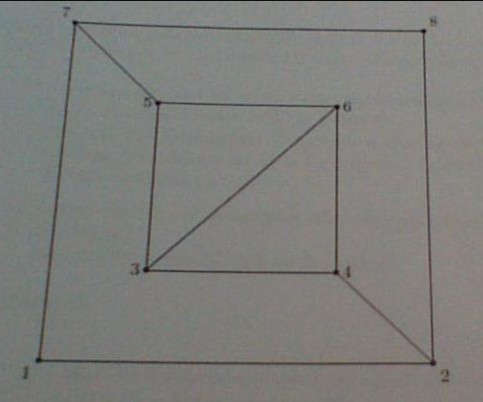
a) Was sind die Zusammenhangskomponenten der Graphen \( G, G-U_{1} \) bzw. \( \left(G-U_{1}\right) \cap\left(G-F_{1}\right) \) aus Aufgabe \( 39 \)?
b) Sei \( G \) ein nicht zusammenhängender Graph (d.h. es gibt mindestens zwei nicht leere Zusammenhangskomponenten). Zeigen Sie, dass das Komplement \( \bar{G} \) zusammenhängend ist.