Tag 6 haben wir nun. Puuh! Schon eine ganze Strecke zurückgelegt. Da bekommt man natürlich Hunger:

Da werden gleich mal die merkwürdigsten Speisen ausprobiert. Aber Hauptsache sie halten unsere Helden bei Kräften. Diese wurde auch gebraucht, denn einer der Radler ging verloren! Unbewaffnet, also ohne Handy, musste er seine Kumpanen suchen und fragte sich bei vorbeifahrenden Autofahrern durch. Aber keine Sorge, es gab ein Happy End und unser verlorenes Schaf wurde wieder aufgesammelt! Übrigens haben wir wieder wie am gestrigen Tag eine zurückgelegte Strecke von 93 km, die wir uns direkt auf der Karte anschauen können.
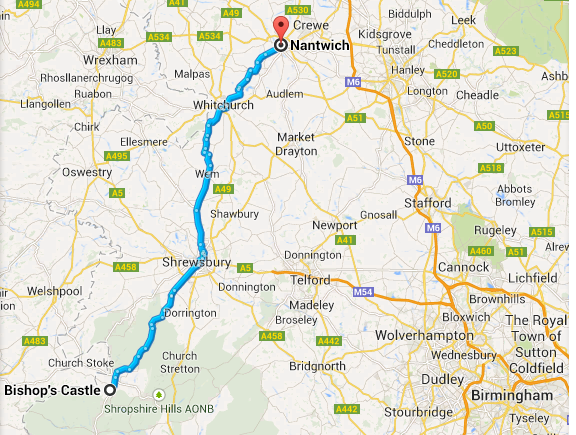
Es geht also immer weiter auf die schottische Grenze zu. Wales (Grenze ist links graugestrichelt zu erkennen) wird bald im Süden gelassen.
Mathe-Challenge (mittel):
Nehmen wir uns doch das „verlorene Schaf-Problem“ mal mathematisch an. Bedeutet so viel wie: Wir gehen davon aus, dass die Radler mit einer Geschwindigkeit von 20 km/h voranfahren. Das verlorene Schaf braucht 10 Minuten bis es registriert, dass es abgehängt wurde. Da man nach mehreren hundert Kilometern nicht mehr voller Kraft strotzt, kann nur eine Geschwindigkeit von 21 km/h erreicht werden, um die anderen einzuholen. Angenommen, dass beide die gleiche Strecke abfahren… wie lange braucht das verlorene Schaf, bis es wieder bei der Gruppe ankommt?
Lösung Mathe-Challenge Tag 5:
Das Volumen der Telefonzelle ergibt sich zu 0,9 m * 0,9 m * 2,51 m^3 = 2,033 m^3. Das entspricht 2033 l. Wenn wir uns nun das Volumen der Radler anschauen, so wissen wir, dass 1 kg = 1 l und damit 4 * 70 l = 280 l.
Damit haben wir 280 l/2033 l= 0,1377 = 13,77 % an durch Menschen verdrängten Volumen und damit 86,23 % an Luftvolumen, und 2033 l - 280 l = 1753 l Luftvolumen. Wir sagten "pro Minute 10 Liter Atemluft pro Person", das bedeutet bei 4 Personen ein Verbrauch von 40 Liter per Minute. Luftvolumen / Verbrauch = 1753 l / 40 l = 43,825 Minuten.