Hi,
Grundlegend ist mir der Sinn des linearen Optimierens nicht bewusst. Ich habe mir bereits einige Videos dazu angesehen. Die waren aber wohl schon sehr viel weiter - es wurde z.B. über Eckpunkte bestimmen gesprochen. Keine Ahnung.
Wir haben in unserem Mathebuch als erstes Thema dazu "Abgrenzung linearer Bereiche". Die ersten beiden Beispiele sind die Graphen zu den linearen Gleichungen: 1. y - 3 > 0 und y - 3 < 0
2. x - 2 > 0 und x - 2 < 0
Hierbei rasten die Graphen ein bei y = 3 und x = 2. Gut, das habe ich verstanden. Auch wenn mir noch nicht bewusst ist, was mir das ganze bringen soll.
Als nächstes Beispiel kommt dann folgende Aufgabe:
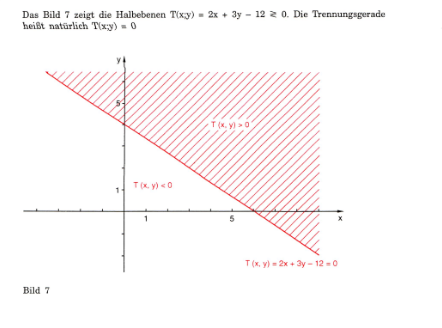
Wie stellt man das für solch eine Lösung um. Bzw. was genau muss ich rechnen / tun, um auf das Ergebnis zu kommen?
Wäre super, wenn mir jemand dieses Beispiel erklären und kurz erwähnen könnte, was mir die lineare Optimierung bringt bzw. wofür sie ist.