Ich nenne den gesuchten Körper eigentlich Quader, nicht Würfel und fasse die einleitende Frage dahingehend auf, dass die Einheit der Antwort cm resp. cm3 sein muss.
Das Volumen des Quaders V = abc , a,b,c Kantenlängen
1. V(x) = (20-2x)(20-2x)x
2. Das maximale Volumen ist abhängig von x, deshalb zuerst x.
3. x finden. V(x) ableiten. Erste Ableitung 0 setzen und so x bestimmen.
3.
V(x) = (400 - 80x + 4x^2) x
V(x) = 400x - 80x^2 + 4x^3
V'(x) = 400 - 160x + 12 x^2 = 0
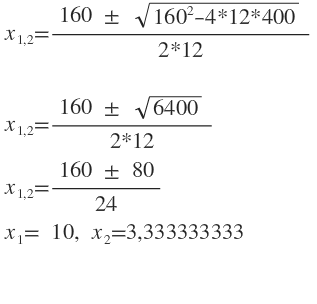
2.
V(x1) = (20-2*10)(20-2*10)*10 = 0 cm3
Ist sicher kein lokales Maximum.
das lokale Maximum muss sich bei x2 befinden.
V(x2) = (20-2*3.3333333333)(20-2*3.333333333)*3.33333333333 = 592,59 cm3 ist das maximale Volumen.
3.
x = 3.333333333 cm ist der zugehörige x-Wert