Binomische Formel von Vektoren: (a-b)² = (a-b)*(a-b) berechnen

Question

a und b sind Vektoren

Berechnen Sie (a-b)² = (a-b)*(a-b)

geg.:

|a| = 2*Wurzel(2)

|b| = 4

Winkel (a,b) =180°

 

Wie muss ich da vorgehen?

Answer 1

|a-b| = 2 * √2 - 4

Das Skalarprodukt  eines Vektors mit sich selber ergibt den Betrag des Vektors im Quadrat.

( 2 * √2 - 4)² =1.3725830020304792191729804126448

Comments

Lu's Lösung ist richtig. Die Vektoren haben entgegengesetzte Richtung. Darum muss man die Beträge addieren, nicht subtrahieren. |a-b| = 2 * √2 + 4. Das Quadrat gibt 46.627417

Answer 2

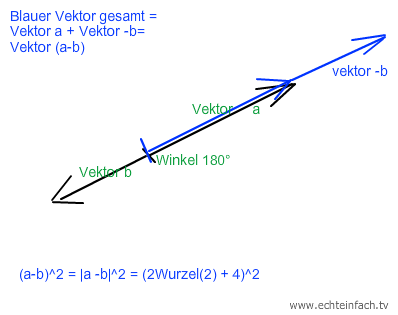
Gemäss Skizze

(a-b)^2 = (2√2  + 4)^2   |vereinfachen so weit du das brauchst.

=8 + 16√2 + 16

= 24 + 16√2

= 8(3 + 2√2)

 

Sollte der Winkel nicht gerade 180° betragen, sollte eigentlich die binomische Formel auch für Skalarprodukte benutzt werden können:

(a-b)^2 = a*a - 2 a*b + b*b = |a|^2  - 2|a||b|cos(Zwischenwinkel) + |b|^2

Du kennst diese Formel bestimmt aus der Trigonometrie als Cosinussatz

c^2 = a^2 + b^2 - 2ab cos (GAMMA)