Ungleichung: 2x^2-4x-16≥0 mit Intervallen und Punktprobe lösen.

Question

2x²-4x-16≥0

Lösungsintervalle:

1. x∈]-∞;x₁[

2. x∈]x₁;x₂[

3. x∈]x₂;∞[

x₁=4

x₂= -2

1. x∈]-∞;4[ zum Beispiel x=2 =

2. x∈]4;-2[ zum Beispiel x=1 =

3. x∈]-2;∞[ zum Beispiel x=-1 =

Answer 1

Hi Emre,

achte bitte auf die Klammerung

1. x∈]-∞;4]

2. x∈[4;-2]

3. x∈[-2;∞[

Diese muss so aussehen. Immerhin gehört die Grenze ja jeweils mit dazu ;).

Wenn Du x = 1 einsetzt, hast Du festgestellen, dass der Wert < 0 ist, sagst aber, dass die Aussage insgesamt stimmt... Auch bei den anderen beiden sind die Aussagen....sehr speziell. Da scheinst Du einfach willkürlich zugeordnet zu haben?! :P


Überhaupt..wie kommst Du darauf von -∞ nach 4 zu laufen und dann auf einmal von 4 zur -2 (also rückwärts). Achte auf den Zahlenstrahl!

Nochmals bitte...die Nullstellen sind richtig, der Rest aber nicht :P.

Comments

woher weißt Du wie man die Klammerum setzt?? So stand es im Internet :)

das ist alles so viel Oo da dreh ich noch durch Oo

---

Dann müsste es aber die Ungleichung gewesen sein:

2x²-4x-16 > 0

und nicht

2x²-4x-16≥0

Und die eine Klammerung bedeutet "inklusive", die andere "exklusive" der Grenze.

1. x∈]-∞;4]

Hier hast Du beides. Links ohne die Grenze (da ∞ keine Zahl ist) und rechts inklusive der 4, da diese explizit ins Intervall gehört ;).

---

es war die zweite...http://www.mathebibel.de/casio-fx-991de-plus-quadratische-ungleichungen-loesen

Ahso ok Danke :)

aber leider verstehe das doch nicht Oo

---

Sehe die Aufgabe da nicht? Zumindest nicht die Lösung. Nur die Aufgabe selbst? :P

---

Ich sehs genauso wie Du :D

Könntest Du mir mal mit LaTex die Lösung aufschreiben? Mit diesen 3 Intervalllösungen?? Bitte das wäre soooooooooooooooooooooooooooooo unglaublich toll, beeindruckend, unglaublich, mega mega toll!!!

---

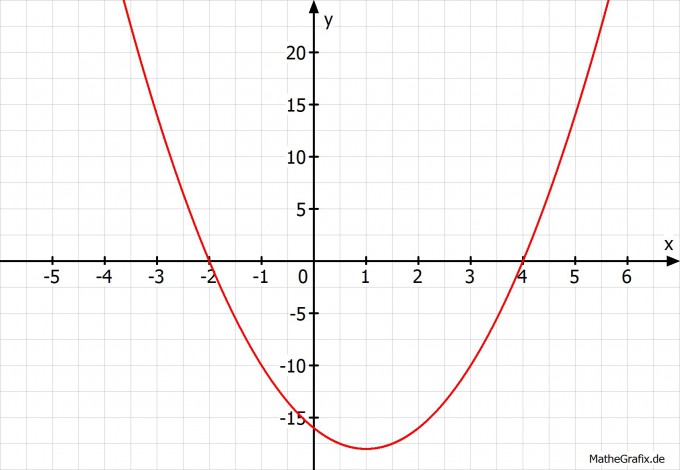
Dann mal so wie ich sie lösen würde:

$$2x^2-4x-16 > 0 \quad|:2$$

$$x^2-2x-8 > 0\quad|\text{pq-Formel}$$

$$x_1 = -2 \text{ und } x_2 = 4$$

------------------------------
Folgendes würde ich nicht tun (bzw. nur im Kopf), aber um Deine Vorgehensweise ein Stück zu adaptieren.

Überlegung, welche interessante Intervalle entstehen

1. \(x\in]-\infty;-2]\)

2. \(x\in[-2;4]\)

3. \(x\in[4;\infty[\)
------------------------------
Eine Punktprobe machen. Das einfachste ist meist x = 0.
Da erhalten wir einen Wert, der kleiner 0 ist. Die Ungleichung ist also nicht erfüllt.
Meine Interpretation:
Die Lösung muss \(x_1 \in ]\infty;-2]\) und \(x_2 \in [4;\infty[\) sein.

Dabei habe ich auch gerne ein Schaubild der Funktion im Kopf um mir klar zu machen, dass eine Punktprobe ausreichend ist:

---

Ich wollte schon vor ner halben Stunde ins Bett. Das hole ich jetzt nach.

Bevor Du weitere Aufgaben hierzu machst, kannst Du das ja mal hier durchlesen: http://mathenexus.zum.de/html/analysis/ungleichungen/weiterfuehrendes/b2_quadUngl.htm

Das sah recht gut aus. Achte auf die Intervallklammern ;).

Gute Nacht

---

Danke :-)

tut mir leid wenn ich dich aufgehalten habe :)

Und Danke für deine große Hilfe!!!

---

Tu es ja gerne.  Aber Schönheit kommt nicht von selbst xd.

Freut mich, wenn ich weiter helfen konnte. ;)

Answer 2

Emre, du machst es dir wieder selbst schwer
weil du von Thema zu Thema hüpfst.

Bei der (Un-)Gleichung  2x²-4x-16≥0
könnte man wie folgt vorgehen.

1.) Ersteinmal die Nullstellen ermitteln indem die
Gleichung geformt wird
2x²-4x-16 = 0
Lösung
x = -2
x = 4

2.) Bei diesen Stellen findet also ein
Wechsel von " postiv nach negativ " oder
" negativ nach positiv " statt.
jetzt schaue ich mir den Funktionswert
in der Mitte zwischen -2 und 4 bei x = 1 an.
f ( 1 ) = 2*1² - 4*1 -16 = -18
Bei x = 1 ist der Funktionswert im " negativen ".

Daraus ergibt sich.
Der Funktionswert  kommt aus dem postiven
Bereich geht bei x = -2 in den negativen Bereich und
geht bei x = 4 wieder in den positiven Bereich.

Die Lösungsmenge für die Aufgabe 2x²-4x-16≥0  ist

L = ( - ≈  bis einschließlich -2  ) und
       ( einschließlcih 4 bis ∞ )

mfg Georg

Comments

Hallo georg,

Wieso schwer?? Ich bleib  jetzt bei diesem thema bis ich das kann!! Hab ich mir vorgenommen :-)