Hallo Chips,
(x - 3)/(x + 3) > 3
1. Fall (x + 3) > 0
Beide Seiten mit (x + 3) multiplizieren ergibt dann
x - 3 > 3 * (x + 3)
x - 3 > 3x + 9 | - x - 9
-12 > 2x | : 2
-6 > x
Aus (x + 3) > 0 folgt aber x > 3
Also gibt es für den ersten Fall keine Lösung.
2. Fall (x + 3) < 0 | also x < -3
Beide Seiten mit (x + 3) multiplizieren ergibt dann
x - 3 < 3 * (x + 3)
x - 3 < 3x + 9 | -x - 9
-12 < 2x
-6 < x
Da nach Annahme gilt x < -3,
ist die Lösungsmenge also
L = {x ∈ ℝ | -6 < x < -3}
Wolfram Alpha kommt auf das gleiche Ergebnis:
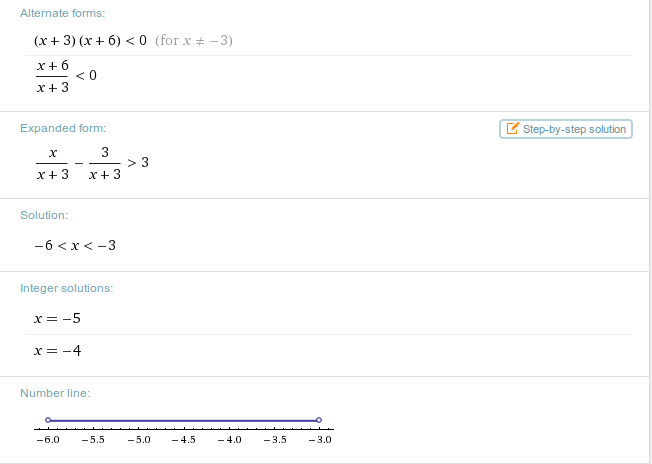
Besten Gruß