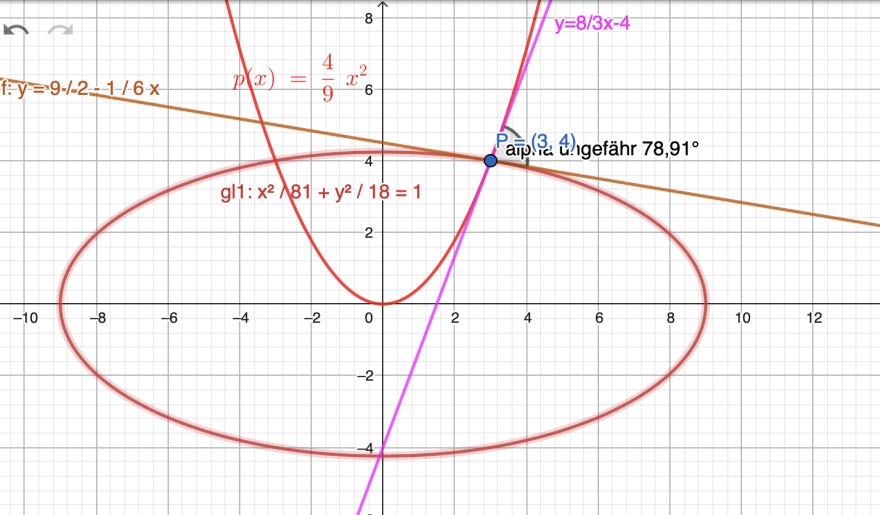
Eine Ellipse mit Brennweite \( e=3\sqrt{7} \) schneidet eine Polynomfunktion. \( y=c x^2 \) im Punkt P\( (3|4)\).
Die Parabelgleichung lautet \( p(x)=\frac{4}{9}x^2 \)
a) Bestimmung der Ellipsengleichung:
\( \frac{x^2}{a^2}+\frac{y^2}{b^2}=1 \) P\( (3|4)\) liegt auf dem Ellipsengraphen.
1.) \( \frac{9}{a^2}+\frac{16}{b^2}=1 \)
Es gilt \( e^2=a^2-b^2 \) → 2.) \( 63=a^2-b^2 \)
Aufgelöst erhält man die Ellipse \( \frac{x^2}{81}+\frac{y^2}{18}=1 \)
b) Bestimmung der Schnittwinkel:
Tangente an Ellipse:
Allgemein: \( \frac{xx_0}{a^2}+\frac{yy_0}{b^2}=1 \)
\( \frac{3x}{81}+\frac{4y}{18}=1 \) → \( y=\frac{9}{2}-\frac{1}{6}x \)
Steigung der Parabeltangenten in P(3|4):
\( p'(x)=\frac{8}{9}x\)
\( p'(3)=\frac{8}{3}\)
\( α=\tan^{-1)}(|\frac{m_2-m_1}{1+m_1m_2}|)\)
\( m_2=\frac{8}{3} \)
\( m_1=-\frac{1}{6} \)
Eingesetzt kommt ein Winkel von ungefähr 78,9° raus.
Das von der Parabel, der Parabeltangente in P und der x-Achse eingeschlossene Flächenstück rotiert um die y-Achse. V=?
Der Teil ist von mir gelöscht worden.(Vielleicht gibt es dafür noch eine schlüssige Antwort. Ich bringe das nicht hin.)
Schreibe dem Ellipsoid, das durch Rotation um die x-Achse entsteht, den volumengrößten Drehkegel ein, dessen Spitze im linken Hauptscheitel der Ellipse liegt.
Planfigur: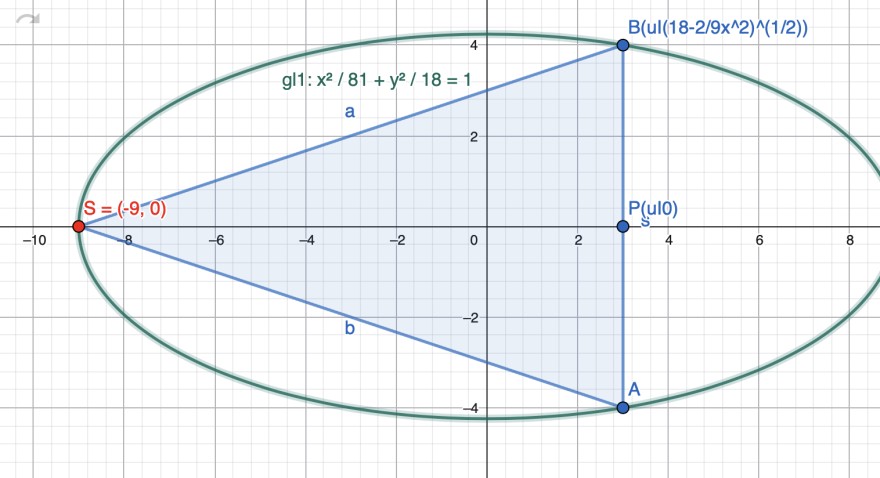
In der Zeichnung muss es \(B(u| (18-\frac{2}{9} u^2 ) ^{\frac{1}{2}} )\)heißen.
V=1/3 π r^2 h soll maximal werden.
V=1/3(18-2/9u^2)(u+9)
V'=1/3π[(-4/9u(u+9)+(18-2/9u^2)]
V'=0
u_1=-9 kommt nicht in Betracht
u_2=3
h=12
r^2=16
V=1/3 π*16*12=64*π VE