Rotationsvolumen. Fläche rotiert um y-Achse

Question

Hallo ,

Ich bräuchte hilfe bei der Berechnung des Volumens von folgender Skizze

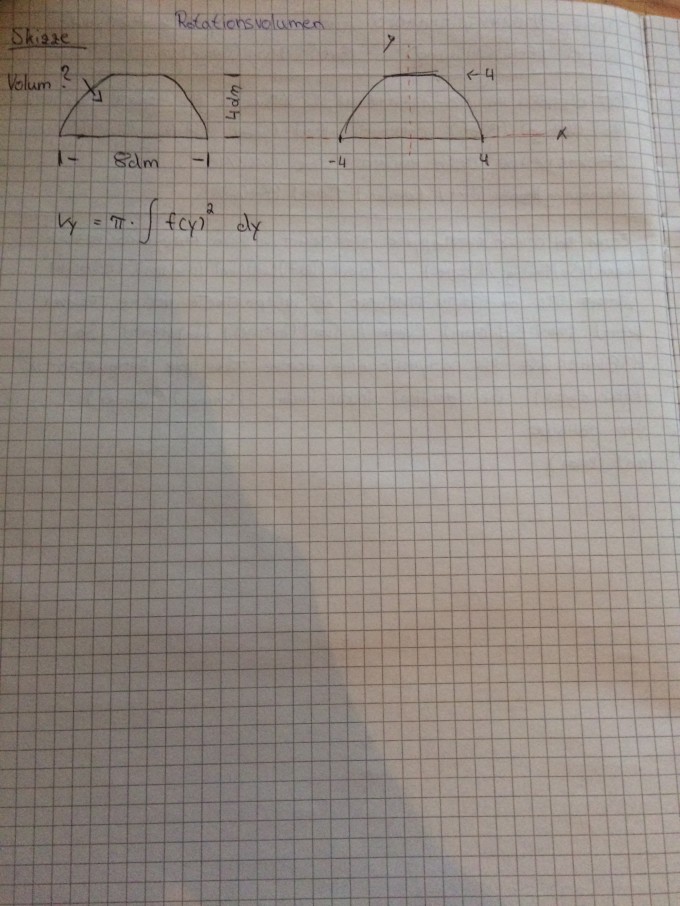
Diese Fläche soll um die y-achse rotiert werden. Da die Angaben nicht reichen um eine explizite quadratische funktion zu errechnen habe ich folgende genommen die die Anforderungen erfüllt die erfüllt werden können(Nullstellen bei x=-4 und x=-4).

f(x)=-0,5x^2+8.

Was ich bis jetzt herausbekommen habe ist dass ich eine Umkehrfunktion brauche.

y=-0,5x^2+8    |-8

y-8=-0,5x^2     |:(-0,5)

-2y+16=x^2     | √

√-2y+16=x      | x und y vertauschen

y= √-2x+16

So habe ich es mit hilfe des Internets gelernt.

Ich habe aber nun ein Video gesehen wo der Schritt mit dem ziehen der Wurzel ausgelassen wurde.

In meiner Aufgabe wäre dann die Umkehrfunktion -2y+16.

Dies wurde nun in die " Formel " eingesetzt für das Rotationsvolumen. Stammfunktion gebildet im entsprechenden Intervall und fertig. Was ist jetzt richtig ?

Mit der Vorgehensweise wie im Video wuerde ich die Aufgabe loesen koennen. Ich koennte jedoch weil mir das wissen fehlt keine stammfunktion von √-2x+16 bilden.

Zuvor muesste ich diese funktion ja mit sich selber nehmen bevor ich eine Stammfunktion bilden muss was für mich auch schwerer ist als von -2y+16.

Wir hatten das Thema noch nicht und auch nicht um die x achse. Wobei es ja nicht so viel zu beachten gibt beim rotieren um die x-achse als um die y-achse

Ich bin am Vorarbeiten und hoffe mir kann jemand helfen.

Ich würde gerne wissen was jetzt genau meine Schritte sind und wenn moeglich ein Ergebnis zur Selbstkontrolle.Oder ob ich komplett falsch liege. Habe gerade wirklich keine Ahnung wie ich dies nun ausrechnen soll !

Ich bedanke mich bis hierhin und für jede kommende Antwort :)

Schönen Abend/Tag noch

Oliver

EDIT(Lu): In der Überschrift "Rotationsfläche" durch "Rotationsvolumen" ersetzt. Da in allen Antworten ein Volumen ausgerechnet wurde. 

Comments

Deine Funktion sieht wie folgt aus:

~plot~ -0,5x^2+8;[[-8|8|-2|10]] ~plot~

Ist das so beabsichtigt?

Bitte stelle doch die Frage im Original zur Verfügung, wie sie dir vorliegt.

---

Das was auf dem Blatt steht ist exakt das was an der Tafel stand. Es gibt keine schriftliche Aufgabenstellung dazu . Wir sollen das Volum berechnen wenn wir um die y-achse drehen

Es soll eine Vase darstellen die umgedreht ist . Sprich de oeffnung hat ein durchmesser von 8dm und eine höhe von 4dm . Die bodenlaenge ist nicht gegeben also habe ich (x-4)(x+4) ausmultipliziert und skalliert damit es der Skizze aehnelt

---

Zur Kontrolle :  Aus deiner Skizze ergibt sich ein Volumen von etwa 111,7 VE.

---

Ich habe 150VE raus.
Habe von Untergrenze=0 bis Obergrenze =4 integriert (-2x16)dx
Das sind 48 mal pi ergibt 150VE

---

111,VE scheind mir etwas falsch zu sein wenn ich das sagen darf.

8*8*4=256. Das wäre die VE von einem Quader mit meinen Längen.

Da meine Vase beim rotieren auf jeden Fall mehr ist als die Hälfte wie von dem Quader muss doch mehr als 128 herauskommen ?

---

111,VE scheind mir etwas falsch zu sein wenn ich das sagen darf.

8*8*4=256. Das wäre die VE von einem Quader mit meinen Längen.

Da meine Vase beim rotieren auf jeden Fall mehr ist als die Hälfte wie von dem Quader muss doch mehr als 128 herauskommen ?

8 * 8 * 4 Wären das Volumen eines umschreibenden Quaders. Ein Quader hat nun aber absolut nichts mit einem rotationsvolumen zu tun. Du könntest einen umschreibenden und einschreibenden Zylinder nehmen.

pi*4^2 * 4 = 201.0619298

pi*2^2 * 4 = 50.26548245

Wobei bei deiner Skizze der untere Radius noch eher kleiner als 2 ist.

Daher kannst du etwas zwischen 50 und 201 VE annehmen. Und 111 klingt da eigentlich recht gut.

Ich habe bei meiner Rechnung den unteren Radius mal mit genau 2 angenommen.

Answer 1

Ich mittel mal etwas zwischen deiner Funktion und der Skizze und nehme den unteren Durchmesser mit 4 LE und den oberen Durchmesser mit 8 LE an.

Comments

Wäre das so im Groben richtig ?

Hab noch große Probleme es Mathematisch korrekt aufzuschreiben!

---

Gerechnet ist das soweit richtig bis auf den Rundungsfehler am Ende.

150.7964473 = 151 VE

Die Stammfunktion schreibt man anders

∫ (a bis b) f(x) dx = [F(x)] (a bis b) = F(b) - F(a)

Den Teil mit den eckigen klammern lasse ich meist weg.

---

Ok dank dir.

Werde es nochmal überarbeiten.

Auf jeden Fall große Hilfe gewesen.

Answer 2

Also... Du hast mit allem recht, was die Umkehrfunktion anbelangt. ^^

Aber du solltest einfach weiterrechnen: Denn du quadrierst die Wurzelfunktion in dem Volumenintegral! Das, was da raus kommt, kannst du nämlich locker, flockig integrieren

Comments

Willkommen in der Mathelounge :-)

Vielleicht als Tipp: Du kannst die MathJax-Befehle nutzen, um die Formeln als Text darzustellen, was mehrere Vorteile hat. Das sieht dann z. B. so aus:

\(x=\sqrt{-2x+16}\)

\(V_R=\pi \cdot \int\limits_{-4}^{4}{(f(x))^2\mathrm{d}x}\)

Viel Erfolg weiterhin!

---

Vorab erstmal danke

Aber darf ich fragen warum von -4 bis 4 ? Ich hätte jetzt gedacht von 0 bis 4 oder von 0 bis -4. Man gibt doch das intervall an was man drehen will oder nicht ?

Also von 0 bis 4 will ich um die y-achse gedreht bekommen.

---

Würdest ja dann nur die Hälfte von der Vase um die Achse rotieren lassen, deshalb von -4 bis 4

---

Falsch. Es muss von y1=0 bis y2=4 über die Umkehrfunktion f(y) integriert werden(von unten nach oben), weil sich der Graph um y-Achse dreht.

Würde ich von y1=-4 bis y2=4 integrieren, dann wäre meine Vase doppelt so hoch, also 8dm.

---

Genau ! Also ich denke so wie " hallo97 ". Wenn ich 4dm rotieren lasse kommen 8dm raus da 4dm ja dann der radius ist. Lasse ich jedoch 8dm rotieren kommen 16dm raus !

Answer 3

Ich schrieb  Aus deiner Skizze ergibt sich  und war von der Skizze des Fragestellers

ausgegangen

Comments

Ok entschuldige dann habe ich es falsch verstanden ! Ich dachte dies sei der VE meiner funktion und nicht meiner Skizze

Wäre dann 150VE richtig bei meiner Funktion ? -0,5x^2+8

Umkehrfunktion =    y=-2x+16

---

Umkehrfunktion =    y=-2x+16 

Das ist nicht die Umkehrfunktion und die wird ja auch gar nicht gebraucht.
Du musst doch nur das Integral  V = π·_(0)∫^4 x^2 dy  berechnen  und wenn 
y  =  -0,5x^2 + 8  ist, dann ist  dy = -x dx  und somit 
V  =  π·_(4)∫^{√8} x^2·(-x) dx  =  -π/4·[x^4]_(4)^{√8}  =  -π/4·(64 - 256)
    =  48π  ≈  150,8

---

Warum wird die Umkehrfunktion nicht gebraucht ? Ich dachte das ist ein muss wenn man um die y-achse drehen will ? 

---

Bei Rotation um die x-Achse  :  V_(x) = π·_(x₁)∫^{x_(2)} y^2 dx  ,

bei Rotation um die y-Achse  :  V_(y) = π·_(y1)∫^{y_(2)} x^2 dy

---

In der Formel taucht die Umkehrfunktion auf. Allerdings als Quadrat. Du brauchst also das Quadrat der Umkehrfunktion.

Aber ich finde es auch schöner wenn man die Umkehrfunktion vorher ermittelt. Wobei es nur die Umkehrfunktion eines Teilintervalls ist.

Ich nehme sogar immer noch das pi mit als Faktor zur Funktion, obwohl man nachher auch einfach das Integral mit pi multiplizieren kann.

---

Ich bedanke mich vorerst für eure Hilfe und Mühe :)

Danke euch

Answer 4

Funktion ( blau ) : -0.5 * x^2 + 8
Umkehrfunktion : √ ( 16 - 2x )
Hier die Graphen

Die Umkehrfunktion soll nun um die
x-Achse rotieren und ergibt wieder die
Ausgangsvase.

Wo ist dein Problem ?
Aufstellen der Stammfunktion
∫ √ ( 16 - 2x ) dx
?

Comments

Wie viel VE wuerden Sie denn herausbekommen wenn Sie diese Aufgabe rechnen ?

---

Ist der Boden der Vase denn nicht flach (wie in deiner Wandtafelskizze)?

Wie lang ist der Durchmesser des Bodens genau?

---

Doch der Boden ist flach.

Der Durchmesser des Bodens war nicht gegeben also sind ja mehrere Funktionen moeglich die die vorliegenden Anforderungen erfüllen koennten .

Ich habe nun die Funktion -0,5x^2+8 genommen. Wenn man von 0 bis 4 integriert ergibt sich ja eine gerade Bodelänge . Richtig ?

---

Die rote Kurve ergibt ein Rotationsvolumen
von 201.

---

Von 0 bis 8 denke ich mal ?

Ich habe bei 0-4  150 raus

---

Von 0 bis 4 ergibt sich 150.8.

---

Danke für deine Hilfe und auch noch die uebersichtliche Zeichnung zwischen beiden Funktionen