Hallo miteinander,
Ich brauche eure Hilfe. Wie ihr vielleicht schon ahnt werden demnächst die ersten Klausuren in Mathe geschrieben ._. und wir haben eine Übung dazu bekommen, die ich schon ziemlich schwierig finde. Vom ersten Blatt kommt nur 1 a und b in der Klausur vor, dann Aufgabe 2 ganz und Aufgabe 3 a und b. Die anderen Aufgaben habe ich erledigt. Bei 1a habe ich auch dazu etwas gezeichnet, zur Lösung bin ich aber nicht gekommen...
Ich hoffe ihr könnt mir helfen...
glatter, knickfreier " Übergang an einer Stelle x_{0}
\( f\left(x_{0}\right)=g\left(x_{0}\right) \quad \) gleiche Funktionswerte
\( f'\left(x_{0}\right)=g^{\prime}\left(x_{0}\right) \quad \) gleiche Steigung
für einen, krümmungsruckfreien" Übergang auch
\( f^{\prime\prime}\left(x_{0}\right)=g^{\prime \prime}\left(x_{0}\right) \quad \)
gleiches Krümmungsverhalten
Aufgabe 1
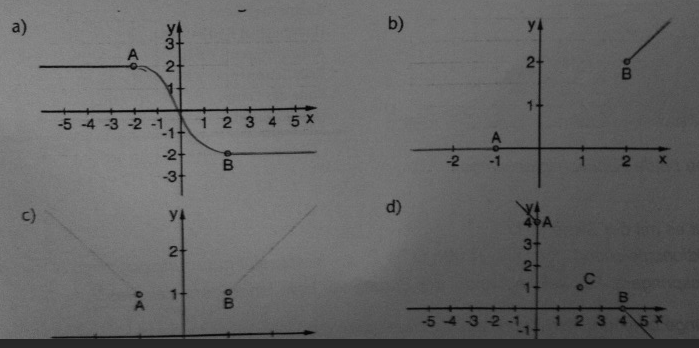
In den folgenden Situationen sollte gute, "knickfreie" Übergangsbögen zwischen A und B gefunden werden. In d) soll dieser Bogen durch den weiteren Punkt C verlaufen. Bestimme jeweils einen passenden Funktionsterm.
Aufgabe 2
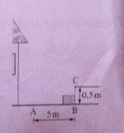
Von einer Garage aus soll eine Auffahrt zur Straße angelegt werden. Der Höhenunterschied beträgt 0,5 m. Die Auffahrt soll in A "glatt" beginnen und in C "glatt" in die Straße einmünden.
a) Beschreibe die Auffahrt durch eine ganzrationale Funktion niedrigsten Grades.
b) Zwischen A und B beginnt 1 m vor C eine 30 cm hohe Festplatte. Wird sie überdeckt?
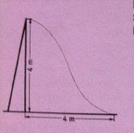
Das nebenstehende Bild zeigt den stark vereinfachten Verlauf einer Metallrutsche für Spielplätze. Das seitliche Profil der rutsche soll durch den Graphen einer ganzrationalen Funktion modelliert werden und durch deren Extrempunkte begrenzt sein.
a) Bestimmen Sie einen geeigneten Funktionsterm.
b) Der TÜV forder von den Herstellern, dass Spielplatzrutschen an keiner Stelle steiler sein dürfen als 50° (gegen die Horizontale). Entspricht die Rutsche dieser Anforderung?
c) Zusatzaufgabe: Entwerfen Sie eine 4m hohe Rutsche, deren Steigung an der steilsten Stelle genau 45° beträgt.
Memo: Zusammenhang zwischen Steigung und Steigungswinkel an einer Stelle x0= m = f'(x0) = tan α