Bestimmung von Funktionstermen: Brückenbogen überspannt 50 m breiten Geländeschnitt.

Question

ich habe mathe lk in der 12.Klasse aber habe eine Aufgabe nicht vertsanden könnt ihr mir die bitte rechnen wäre :

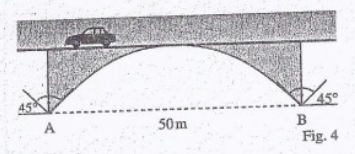
Ein Brückenbogen überspannt einen 50m breiten Geländeeinschnitt.In A und B setzt der Bogen senkrecht an den Böschungen auf (Fig4.)(sieh unten).

a)Beschreiben Sie die Form des Brückenbogens durch eine ganzrationale Funktion zweiten Grades.

b)Wie hoch wird der Brückenbogen?

Lösung:

a)Koordiatensystem:Siehe Fig. 5(?keine Ahnung wo die sein soll auf meinen Ab ist das nicht),

Ursprung in der Mitte M der Strecke AB.

Vertsehe die Aufgabe irgendwie nicht,

danke euch

Comments

Das Koordinatensystem kannst Du einfach drüberwerfen wie ein Netz über den Schmetterling. Sinnvoll ist einen günstigen Ursprung zu wählen.

---

eine Rechnung wäre besser da ich das überhaupt nicht checke,dies ist eine Übungsaufgabe für die Klausur

---

Mitmachen bei der Erarbeitung der Vorgehensweise wäre noch besser, weil Du sonst bei der nächsten Aufgabe gleicher Art wieder wie ein Ochs vorm Scheunentor stehst. Wenn Du die Aufgabe bis zu Ende gelesen hättest, wüsstest Du sogar, wo der Ursprung liegen sollte.

---

Höhe Brückenbogen -----> tan α = 25 / x → x = 25 / tan 45° = 25 / 1= 25 m !

---

ich glaube das stimmt nicht, weil die 45° sind die Tangentensteigung und nicht die Steigung vom Eckpunkt zum Hochpunkt....

---

richtig ! Aus der Steigung der Tangente kann man auf den Wert der ersten Ableitung in diesem Punkt schliessen. Ausserdem haben wir auch schon die Nullstellen dank der geschickten Positionierung des Ursprunges, die dann ja nur noch in die Linearfaktoren eingesetzt werden müssen.

---

Das ist ein Beispiel mit durchgerechneter Lösung direkt darunter.

---

warum wurde hier eigentlich die steigung mit tang und nicht mit sin oder cos berechnet? danke im voraus...

---

Wenn man an eine Funktion im Punkt \(A\) eine Tangente (blau) anlegt, so ist die Steigung \(m\) definiert als die Strecke, die die Tangente in Y-Richtung ansteigt (von \(C\) nach \(B\)), wenn man sich in X-Richtung um 1 bewegt (von \(A\) nach \(C\)).

Der Tangens des Steigungswinkels \(\alpha\) (blau) ist

$$\tan \alpha = \frac{\text{Gegenkathete}}{\text{Ankathete}} = \frac{m}{1}=m $$

PS.: "danke im voraus..." ist nie gut. Besser nachher Feedback geben.

---

danke zunächst einmal für die anschauliche Darstellung, mit welchem Programm hast du den die eigentlich gemacht, wäre bereit dieses auch zu benutzen. Ja, ich danke gerne im voraus, weil ich bisher noch keine schlechten Antworten innerhalb dieses Forums bekommen habe.

---

mit welchem Programm hast du den die eigentlich gemacht

mit Cinderella - siehe https://cinderella.de

---

danke, das wird mir sicherlich in naher Zukunft beim Umgang mit der Mathematik weiterhelfen.

Answer 1

Symmetrie bei

f ( x ) = a * x^2 + b
f ´( x ) = 2 * a * x
rechte Seite
f ´( 25 ) = 2 * a * 25 = - tan ( 45 )
2 * a * 25 = -1
a = -0.02

f ( x ) = -0.02 * x^2 + b
f ( 25 ) = -0.02 * 25^2 + b = 0
-0.02 * 25^2 + b = 0
b = 12.5

f ( x ) = -0.02 * x^2 + 12.5

Der Bogen hat eine Höhe von 12.5 m.

Comments

2.Grad lautet doch ax^2+bx+c

---

hallo ich mach momentan dieselbe aufgabe, jedoch verstehe ich eine sache nicht und zwar:wie bist du aus -tan(45) gekommen? ich weiß, dass m=tan (in diesem fall von 45) ist aber warum das minus??

---

Ich gehe vom rechten Auflager aus.
Dort ist der Winkel 45 ° für die Steigung der Böschung
eingezeichnet.
Das andere Zeichen ist wohl ein rechter Winkel.
Also bleibt 45 ° für den restlichen Winkel übrig.
Wird das Koordinatensystem als mittig zur Parabel
angenommen ist der Winkel bei x = 25 m gleich
45 ° abfallend.
m = - tan ( 45 ) = -1
oder
m = tan ( -45 ) = -1

---

Warum setzt man das mit tan(45) gleich wie kommt man darauf?

---

In der Aufgabe steht doch
45 ° Böschungswinkel
und
der Pfeiler setzt senkrecht ( 90 ° ) dazu auf

180 ist der Gesamtwinkel unten. Also
180 - 45 - 90 = 45 °

Es bleiben 45 ° für den Bogenwinkel übrig.
Der Winkel ist am linken Auflager steigend . Also 45 °. m = tan(45)
Der Winkel ist am rechten Auflager fallend. Also -45 ° m = tan(-45)

Answer 2

f(x) = a - b·x^2

f(25) = 0
a - 625·b = 0

f'(25) = -1
- 50·b = -1

Wir lösen das LGS und erhalten a = 12.5 ∧ b = 0.02

f(x) = 12.5 - 0.02·x^2

Answer 3

Wenn du den Urspung in die Mitte von der Strecke AB legen sollst, sieht das ca so aus:

Auf die -25 bis 25 bin ich gekommen, weil die Strecke 50 lang ist.

Außerdem steht in der Aufgabenstellung noch folgende Information:

Die Brücke ist eine Funktion 2. Grades also kann man allgemein annehmen, dass die Funktion folgende Form hat: f(x)=ax^2+bx+c

Am Boden setzt die Grücke senkrecht an der Böschung an. Damit kennst du was über die Steigung der Tangenten in diesen Punkten.

Hilft dir das schon weiter? Wenn nicht melde dich nochmal