Integral tanx mit -pi < x < pi

Question

Problem beim Verstehen der Lösung:

Das Integral von tan(x) kann ich lösen, es ist -ln|cosx| + C

Jetzt ist mein Problem mit den Betragsstrichen.

In der Aufgabe wird explizit gesagt: x ∈(-π, +π)

Es sind offene Grenzen also heisst das doch -pi < x < +pi

Kann ich dann die Betragsstriche weglassen bei -ln|cosx| + C für diese Voraussetzung?

In der Lösung wird gesagt: -ln(cos x)

cos x > 0

Aber wenn ich mir den cosx anschaue als Graphen

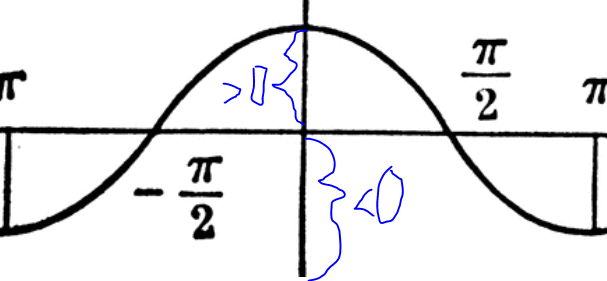
Der Funktionswert f(x)=y kann doch sehr wohl < 0 werden? und zwar im Intervall x ∈ [-pi, -pi/2)

Wo ist der Denkfehler? Der Betrag muss verschwinden, weil das Integral als Exponent in der e-Funktion steht.

Answer 1

Die Aufgabe erscheint mir etwas unsinnig. Tan(x) ist eine Punktsymmetrische Funktion. 

Das Integral in symmetrischen Grenzen um den Ursprung muss 0 sein.

Weiterhin wird hier aber über Polstellen einfach hinweg integriert was sicher eigentlich nicht so sein darf.

Comments

pi und -pi sind nicht die Integrationsgrenzen.

Es geht hier nur um die Stammfunktion! Also kein b oder a vorhanden.

Ich will nur wissen ob das richtig ist, was in der Lösung steht.

---

"Der Betrag muss verschwinden, weil das Integral als Exponent in der e-Funktion steht. "

Bei der Aussage habe ich ohnehin Schwierigkeiten. Wo haben wir hier eine e-Funktion? Vielleicht veröffentlichst du mal die gesamte Aufgabe und nicht nur einen Auszug davon. Vielleicht kann man dann sehen worauf die Aufgabe hinaus will.

---

Das Integral steht im Exponenten und die Stammfunktion ist gesucht und soll die e-Funktion aufheben.

e^∫tanxdx

---

Die Stammfunktion von TAN(x) ist eigentlich -LN(COS(x)). COS(x) muss aber größer 0 sein weswegen hier nur Werte von ]-pi/2 ; pi/2[ für x erlaubt wären. Selbst pi/2 ist ja nicht erlaubt wegen der Polstelle.

Will man andere Grenzen haben weswegen auch immer kann man den Betrag vom COS(x) nehmen. 

---

Ich hab nur das Integral gepostet, wegen der Betragsfunktion im ln und der Aussage in der Lösung

---

Ist denn die Aussage im Bild (Lösung) also richtig oder falsch? 

Zur Info:

In der Lösung wird dann einfach die Betragsfunktion weggelassen und man rechnet weiter mit

e^ln(1/cosx)

---

Nur hier ist cosx > 0 , oder?

---

Dann sind die Grenzen in der Lösung nur verkehrt. Dann sollten die Grenzen ]-pi/2 ; pi/2[ sein. Denn nur dort ist der COS(x) > 0.

---

Noch eine Frage: Im oben genannten Intervall ist das doch eine Periode vom cosx oder? Also eine Schwingung

---

Das wären ja 2pi