Trapezeigenschaften mittels Vektorrechnung zeigen

Question

Aufgabe:

In jedem Trapez, das kein Parallelogramm ist, liegen die Mittelpunkte der Grundseiten und der Schnittpunkt der verlängerten Schenkel auf ein und derselben Geraden.

Meine Lösung:

Ist mein Vorgehen so korrekt und ausreichend?

Comments

Für einen Schüler dürfte das reichen. Für einen Studenten kaum. 

Von einem Studenten würde man eine schöne Formelmäßige Herleitung erwarten, so in etwa wie es dir neulich an einem schönen Beispiel gezeigt worden ist.

---

Vorschlag : D = C + c( A - B) / A - B  !

---

Danke, das beruhigt mich - es ist für eine Schülerin :-)

---

auch von einem Schüler wird mehr erwartet

---

@mathe 12:

Danke für die Antwort; ich kann sie aber leider nicht nachvollziehen:

Wie ist damit gezeigt, dass M_AB, M_DC und S auf einer Geraden liegen?

Besten Gruß

---

Wie sähe denn eine schöne formelmäßige Herleitung aus?

---

Was ist "das große", was ist "das kleine Dreieck" ?

Wie werden darauf Strahlensätze angewandt ?   Mit welchem Ergebnis ? 

Der angegebene Vektor wird sicherlich nicht angesetzt um zu S zu gelangen, allenfalls ein Vielfaches davon.  Das "also" in diesem Satz ist völlig unbegründet.

Letzten Endes muss nachgewiesen werden, dass die Skizze nicht in Wirklichkeit so

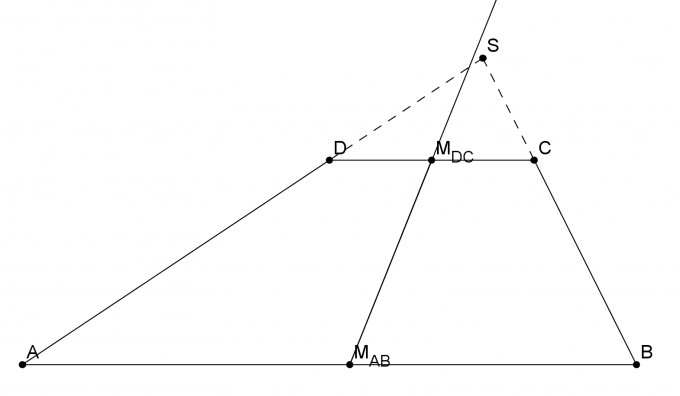
aussieht. Das leistet dein "Beweis" überhaupt nicht.

Schließlich :  Vom Schüler wird lt. Aufgabenstellung Vektorrechnun verlangt, nicht eine Argumentation über ähnliche Dreiecke.

---

@Gast hj219:

Ich danke Dir. 

P.S.:

So kann die Skizze übrigens nicht aussehen, da M_AB in dieser nicht Mittelpunkt der Grundseite AB ist.

---

Warum Mit dem Strahlensatz ist doch alles gesagt

SM_DC / SM_AB = DM_DC / AM_AB

SM_DC / SM_AB = CM_DC / BM_AB

Nun ist aber DM_DC = CM_DC und AM_AB = BM_AB weil M_DC und M_AB ja die Mittelpunkte sind.

Somit ist das Verhältnis von SM_DC / SM_AB in beiden Dreiecken (links und rechts der Seitenhalbierenden gleich).

Das sollte meiner Meinung nach auslangen.

---

Was man aber bemängeln könnte ist, dass es so eben nicht mit der Vektorrechnung gezeigt ist.

---

@Mathecoach:

Sieht sehr gut aus; danke für Deine Mühe!!

---

so geht es eben gerade nicht !

In deiner ersten Gleichung ist S der Schnittpunkt der Geraden AD und M_ABM_DC ,  in deiner zweiten Gleichung ist S der Schnittpunkt der Geraden BC und M_ABM_DC.  Dass diese beiden Schnittpunkte identisch sind, soll gerade nachgewiesen werden und darf eben keinesfalls vorausgesetzt werden.

---

@ Gast hj219:

Ich gebe Dir Recht, sehe allerdings nicht, wie ich einen sauberen Beweis mittels Vektorrechnung hinbekomme.

Weil ich von vorneherein ein schlechtes Gefühl bei meinem "Beweis" hatte, habe ich diese Frage ja hier gepostet.

Jetzt weiß ich also, dass mein Vorgehen nicht ausreichend war, bin aber ansonsten "als klug als wie zuvor" ...

---

Das verstehe ich nicht. 

Ich habe doch gezeigt das das Verhältnis SM_DC / SM_AB in beiden Dreiecken das gleiche ist. Damit ist aber das S eindeutig bestimmt und identisch in beiden Dreiecken.

---

du hast gezeigt, dass EM_DC  / EM_AB  =  FM_DC  / FM_AB   ist, aber noch nicht, wieso daraus E = F  folgt.

---

Na, wenn es nur darum geht... 

EM_AB / EM_DC =  FM_AB / FM_DC

(EM_DC + M_DCM_AB) / EM_DC =  (FM_DC + M_DCM_AB) / FM_DC

1 + M_DCM_AB / EM_DC = 1 + M_DCM_AB / FM_DC

M_DCM_AB / EM_DC = M_DCM_AB / FM_DC

EM_DC = FM_DC