die notwendige Bedingung für einen Extremwert an einer gewissen Stelle ist, wie Du richtig geschrieben hast,
f'(x) = 0
In Deinem Beispiel:
f(x) = 2x2
f'(x) = 4x
Notwendige Bedingung für einen Extremwert ist also
f'(x) = 4x = 0
x = 0
Also haben wir an der Stelle x = 0 einen Kandidaten für einen Extremwert.
Die notwendige Bedingung muss in jedem Fall erfüllt sein, damit wir eventuell einen Extremwert an der fraglichen Stelle haben.
Wenn dann also die notwendige Bedingung erfüllt ist, müssen wir noch die hinreichende Bedingung überprüfen, also
f''(x) < 0 oder f''(x) > 0
Für f''(x) < 0 erhalten wir ein lokales Maximum, für f''(x) > 0 erhalten wir ein lokales Minimum.
Wie Du richtig gerechnet hast, ist
f''(x) = 4, also auch f''(0) = 4 > 0 => lokales Minimum an der Stelle x = 4.
Was dahinter steckt, ist Folgendes:
Du brauchst auf jeden Fall zunächst die notwendige Bedingung f'(x) = 0, um einen Kandidaten für eine Extremstelle zu haben.
EDIT: Ab dieser Stelle auf Hinweis von Gast hj219 korrigiert:
Wenn allerdings die 2. Ableitung f''(x) = 0 ist (also nicht größer oder kleiner als 0), kann es sein, dass kein Extremwert an dieser Stelle vorliegt.
Nehmen wir als Beispiel
f(x) = x3
f'(x) = 3x2
3x2 = 0
x = 0
Aber jetzt:
f''(x) = 6x
f''(0) = 6 * 0 = 0
Wir hatten zwar den Kandidaten x = 0 für einen Extremwert, aber da die 2. Ableitung für x = 0 ebenfalls = 0 ist, liegt an der Stelle x = 0 kein Extremwert vor, sondern ein Wendepunkt!
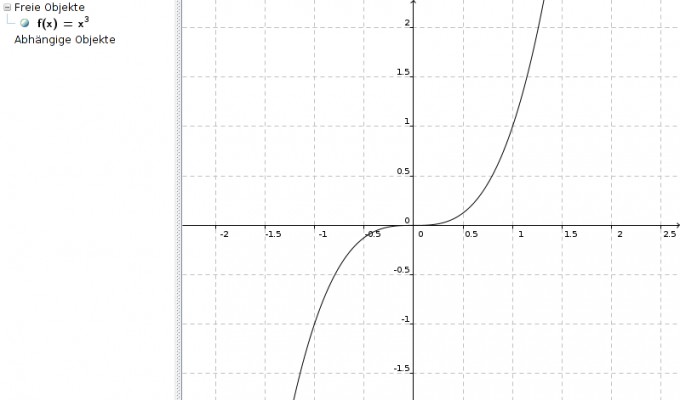
Umgekehrt ist es möglich, dass an einer bestimmten Stelle f'(x) = 0 ist (notwendige Bedingung für Wendepunkt), f''(x) ebenfalls 0 ist und trotzdem ein lokales Extremum vorliegt:
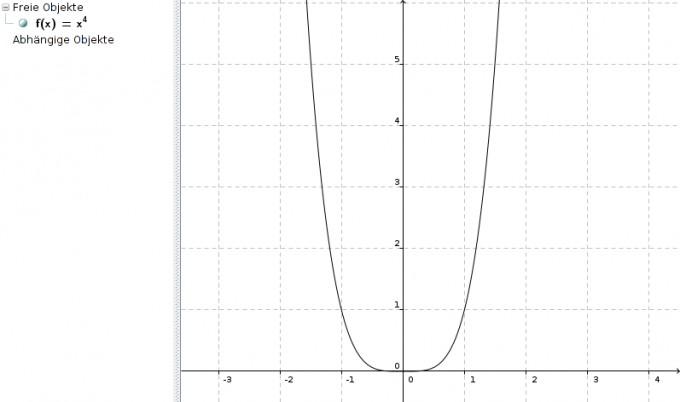
f(x) = x4
f'(x) = 4x3
f''(x) = 12x2
f'(0) = 0
f''(0) = 0
An der Stelle x = 0 liegt ein Minimum vor.
Ich hoffe, ich konnte ein wenig helfen :-)
Besten Gruß