Unter welchem Winkel schneidet die Kurve der Funktion die x-Achse?

Question

Gegeben: \( x(t)=-e^{-2 t}+1,5 e^{-5 t} \) stark gedämpfte Schwingung \( x \) Amplitude, \( t \) Zeit, \( t \geq 0 \)

Gesucht: Unter welchem Winkel schneidet die Kurve der Funktion die x-Achse?

Answer 1

Deine Frage ist aber eine andere als die im gedruckten Text
gestellte Frage.
Nullstelle
-e^{-2t} + 1.5 * e^{-5t} = 0
1.5 * e^{-5t} =  e^{-2t}   |  ln ()
ln ( 1.5 * e^{-5t} ) =  ln ( e^{-2t} )
ln ( 1.5 ) + ln ( e^{-5t} ) ) =  -2t
ln ( 1.5 ) + ( -5t ) = -2t
ln ( 1.5 ) = 3t
3t = ln (1.5 )
t = 0.1352
Probe
-e^{-2t} + 1.5 * e^{-5t} = 0
-e^{-2*0.1352} + 1.5 * e^{-5*0.1352} = 0
-e^-0.2704 + 1.5 * e^{-0.676} = 0
-0.763 + 0.763 = 0  | stimmt

Answer 2

Hi, am einfachsten wird es wohl sein, die Funktion gleich null zu setzen und die Gleichung dann mit e^2t zu multiplizieren.

Comments

Dieser Weg ist sogar eleganter:

$$-e^{-2t} + 1.5 \cdot  e^{-5t }= 0 | \cdot e^{2t}$$
$$-1 + 1.5 \cdot  e^{-3t }= 0 | +1 $$
$$ 1.5 \cdot  e^{-3t }= 1 | \cdot \frac23 $$
$$  e^{-3t }=  \frac23 | ln $$
$$  ln(e^{-3t })= ln \frac23 $$
$$  -3 \cdot ln(e^{t })= ln \frac23 $$
$$  t= -\frac13 \cdot ln \frac23 $$

Answer 3

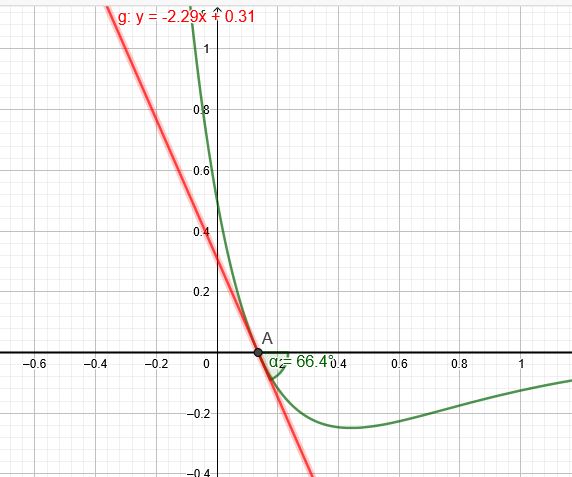
\( f(t)=-e^{-2 t}+1,5 e^{-5 t} \)

Nullstelle bei \(t = 0,1352\) übernommen von "georgborn"

\( f'(t)=-e^{-2 t}\cdot(-2)+1,5 e^{-5 t} \cdot (-5) \)

\( f'(t)=2e^{-2 t}-7,5 e^{-5 t} \)

\( f'(0,1352)=2e^{-2\cdot 0,1352}-7,5 e^{-5\cdot 0,1352}≈-2,29 \)

\( \tan^{-1}(-2,29)=- 66,41°\)