Polynom dritten Grades bestimmen. p(0) = 1/4, lokales Extremum bei x=-1, g(x)=x+1 ist Tangente...

Question

Ich komme mit dieser Aufgabe nicht weiter. Könnt ihr mir helfen ?



Gesucht ist das Polynom dritten Grades p(x) mit den Eigenschaften:


a) p(0) = 1/4

b) p(x) hat ein x = - 1 ein lokales Extremum.

c) Die Gerade g(x) = x +1 ist Tangente an die Kurve für x = 1.

d) Welches Extremum liegt b. vor ?


!


lg

Answer 1

f(0) = 1/4   (Aus Angabe a) )

f'(-1) = 0    (Aus b) Bedingung für Extremum)

f'(1) = 1     (Aus c) Steigung muss dieselbe sein wie an der Tangente)

f(1) = 2     (Aus c) Tangente geht ja an x = 1 durch f(1). Das gilt auch für das Polynom)

Gleichungssystem:

d = 1/4

3a - 2b + c = 0

3a + 2b + c = 1

a + b + c + d = 2

--> f(x) = -0,5x^3 + 0,25x^2 + 2x + 0,25

Für d) Bestimme die Art des Extremums. Zur Kontrolle: Minimum bei (-1|-1)

Grüße

Answer 2

Polynom 3. Grades (ich nenne es aus Gewohnheit f(x)):

f(x) = ax³ + bx² + cx + d

f'(x) = 3ax² + 2bx + c

f''(x) = 6ax + 2b

f(0) = d = 1/4

f'(-1) = 3a - 2b + c = 0

f(1) = a + b + c + d = 2

f'(1) = 3a + 2b + c = 1

a = -0,5

b = 0,25

c = 2

d = 0,25

Die Funktion lautet also

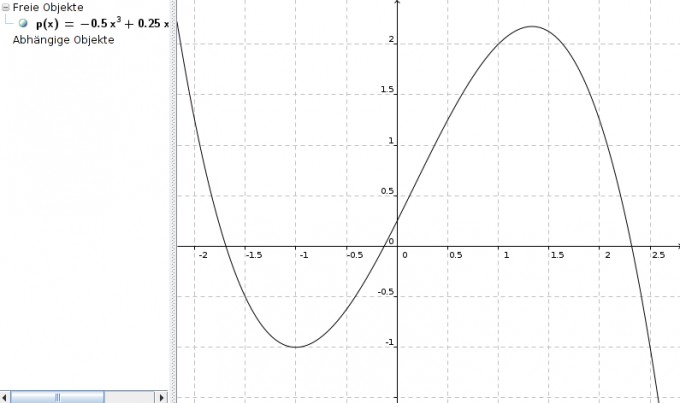
p(x) = -0,5x³ + 0,25x² + 2x + 0,25

p'(x) = -1,5x² + 0,5x + 2

p''(x) = -3x + 0,5 | p''(-1) = 3 + 0,5 = 3,5 > 0; an der Stelle x = -1 liegt demnach ein lokales Minimum vor.

Besten Gruß