Eine Funktion hat bei x=1 eine sowohl Nullstelle wie auch ein lokales Minimum. Wie bestimme ich diese Funktion?

Question

Eine Funktion hat bei x=1 eine sowohl Nullstelle wie auch ein lokales Minimum.

Wie bestimme ich eine oder mehrere solche Funktionen?

 

Nachtrag: Präzision:

Funktionen vom Typ f(x) = ax³+ bx² + cx + d

Comments

Könntest du noch angeben, welche Funktionen bei euch in Frage kommen?

---

Funktionen vom Typ f(x) = ax hoch3 + bx hoch 2 + cx + d

---

Sollst du hier alle diese Funktionen bestimmen? Wenn ja, muss ich das in der Aufgabenstellung noch ergänzen.

Answer 1

So allgemein kann man die folgenden Gleichungen angeben:

Eine Funktion hat bei x=1 eine sowohl Nullstelle

f(1) = 0

wie auch ein lokales Minimum.

f ' (1) = 0 und

Zudem: f ' hat an der Stelle 1 eine Vorzeichenwechsel von - zu +. Oft genügt f '' (1) > 0

 

Das einfachste Beispiel aber bei weitem nicht die einzige Funktion ist hier die Funktion f(x) = (x-1)²

Comments

Ok, danke. Wie bestimme ich eine solche Lösung? Durch Raten, Ausprobieren, Erfahrung, oder gibt es einen analytischen Weg?

---

D.h. wie gehe ich den Schritt von f(1) = 0 und f`(1) = 0 auf f(x) = (x-1) hoch2?

---

Irgendetwas musst du hier vorher schon wissen.

Z.B. dass die Normalparabel y = x² eine Minimalstelle in (0/0) hat.

Dann kannst du sie so verschieben, dass die Minimalstelle in (1/0) liegt.

Das geht, indem du x durch x-1 ersetzt.

Somit: y = (x-1)²

Natürlich kannst du auch den Ansatz machen

1.        y = x² + bx + c

2.       y' = 2x + b

Und jetzt b und c berechnen, durch einsetzen von 0 und 1:

1.    0 = 1 + b + c

2.     0 = 2 + b              

------> b = -2 , c = 1

Also y = x² - 2x + 1 

 

 

 

 

---

Wie komme ich vom allgemeinen Ansatz y= ax²+bx+c auf y=x²+bx+c, d.h.nach welcher Regel wird hier a=1 gesetzt?

---

Ich suche ja eine möglichst einfache Funktion und weiss, dass a> 0 sein muss, wenn da ein Minimum und nicht ein Maximum rauskommen soll.

Allgemeiner kannst du natürlich a>0 voraussetzen und dann

mit viel Algebra (gute Übung!)

y = a(x-1)²  = ax² - 2ax + a         mit a > 0

berechnen

---

Folgende Punkte verstehe ich nicht: 1) Warum muss a größer Null sein, wenn ein Minimum rauskommen soll? 2) Wie komme ich bei der Suche nach einer "möglichst einfachen Funktion" ausgerechnet auf a=1 (und nicht auf a= 2 oder 3 oder ...)? Wie komme ich im obigen Ansatz mit a größer Null vom bisher weiter diskutierten 2. Lösungsweg auf y= a(x-1)hoch 2??

---

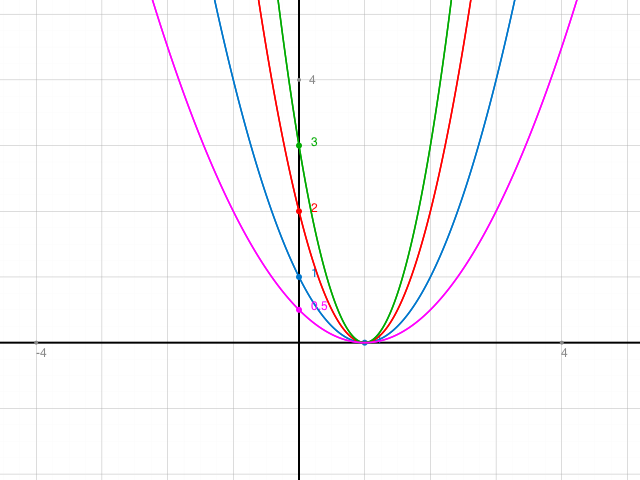
1) und 3) Hier ist mal eine Skizze für a = 0.5, 1, 2 und 3 für y = ax² - 2ax + a = a(x-1)² 

Sobald a<0 ist, kommt es zu einer Spiegelung an der y- Achse; da liegt dann automatisch ein Maximum vor.

2) Rechnen mit 1 wird als einfacher betrachtet als mit 2, 3 oder 0.5.

 

3)  Das Folgende liegt an den binomischen Formeln: y = ax² - 2ax + a = a(x-1)²  

Wenn du ganzrationale Funktionen kennst,

weisst du, dass man Nullstellen faktorisieren kann.

y=a(x-x₁)(x-x₂)(x-x₃)…

Doppelte Nullstellen treten in der Faktorisierung hoch 2 auf.

Zu k-fachen Nullstellen (also hoch k in der Faktorzerlegung) könntest du wissen:

k ungerade: y-Achse wird vom Graph überschritten,

k gerade: y-Achse wird nicht überschritten.

Deshalb hier der Ansatz mit doppelter Nullstelle in x₁=x₂=1.

y=a(x-1)(x-1)