Die Parallelschnittfläche einer quadratischen Pyramide ist ein rechtwinkliges gleichschenkliges Dreieck mit der Kathetenlänge 12,8cm. Wie groß ist die Oberfläche der Pyramide?
Schnitt durch Pyramide:
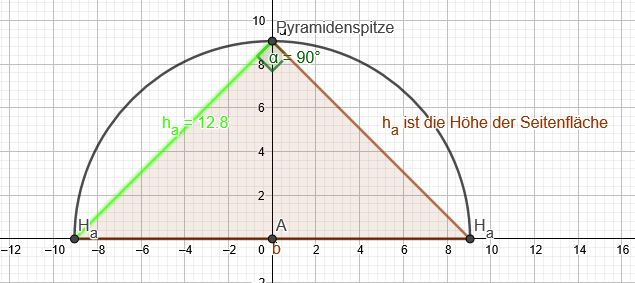
Oberfläche der Pyramide: Grundfläche plus Mantelfläche
Grundfläche: \(A_G=a^2\)
eine Dreieck-Seitenfläche: \(A_D=\frac{1}{2} \cdot a\cdot h_a \)
Mantelfläche: \(A_M=4A_D=4\cdot \frac{1}{2} \cdot a\cdot h_a=2a\cdot h_a\)
Oberfläche der Pyramide: \(O_P=A_G+A_M=a^2+2a\cdot h_a=a(a+2\cdot h_a)\)
Grundseite \(a=\sqrt{h_a^2+h_a^2}=\sqrt{2h_a^2}=\sqrt{2\cdot 12,8^2 }≈18,1\)cm
\(O_P≈18,1 \cdot (18,1+2\cdot 12,8)=790,97\)cm^2
