Funktion und Ableitungen
f(x) = x^4 + 4·a·x^2 + 3·a^2
f'(x) = 4·x^3 + 8·a·x
f''(x) = 12·x^2 + 8·a
Definitionsbereich
D = R
Symmetrie
Achsensymmetrie zur y-Achse, weil x nur in geraden Potenzen auftritt.
Grenzwerte
lim (x → -∞) f(x) = ∞
lim (x → ∞) f(x) = ∞
Y-Achsenabschnitt f(0)
f(0) = 3·a^2
Nullstellen f(x) = 0
x^4 + 4·a·x^2 + 3·a^2 = 0 Substitution z = x^2
z^2 + 4·a·z + 3·a^2 = 0
z = - 3·a ∨ z = -a Resubstitution x = ± √z
x1/2 = ± √(- a)
x3/4 = ± √(- 3·a)
Es gibt also nur Nullstellen für a ≤ 0.
Extrempunkte f'(x) = 0
4·x^3 + 8·a·x = 4·x·(x^2 + 2·a) = 0
x1 = 0
x2/3 = ± √(- 2·a)
f(0) = 3·a^2 --> Hochpunkt
f(± √(- 2·a)) = - a^2 --> Tiefpunkte
Für a ≥ 0 gibt es nur einen Tiefpunkt bei (0 | 3·a^2)
Wendepunkte f''(x) = 0
12·x^2 + 8·a = 0
x1/2 = ± √(- 2/3·a)
f(± √(- 2/3·a)) = 7/9·a^2 --> Wendepunkte
Es gibt also nur Wendepunkte für a ≤ 0.
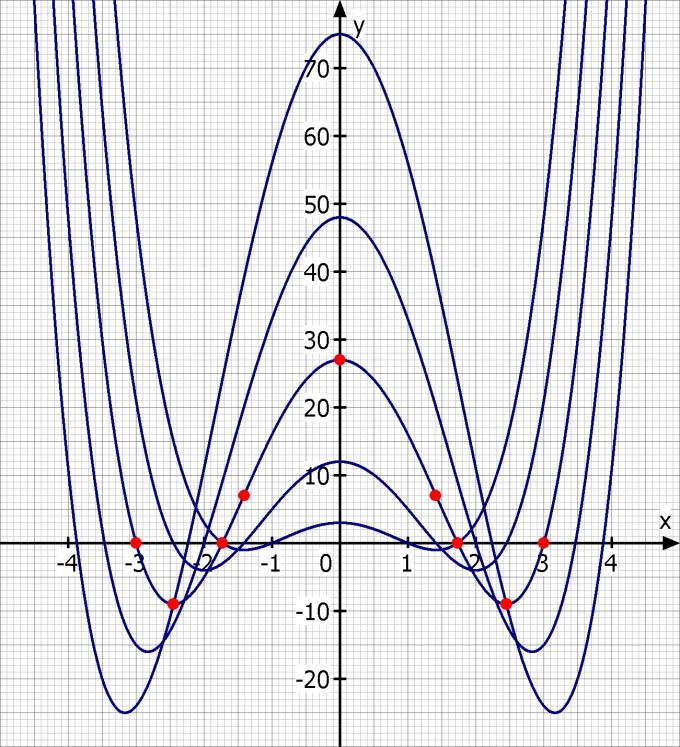
Skizze
Ich habe die Graphen für a = -1 bis a = -5 skizziert und für a = -3 auch die errechneten Punkte eingetragen.