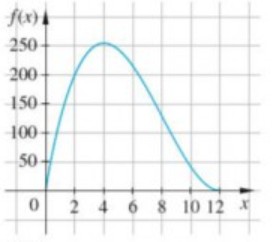
Der Graph der abgebildeten Funktion \( f \) dritten Grades geht durch den Ursprung des Koordinatensystems und hat im Wendepunkt \( W\left(8 \mid y_{w}\right) \) die Wendetangente \( t \) mit \( t(x)=-48 x+512 \)
Die Funktion \( f \) beschreibt näherungsweise die Zuflussgeschwindigkeit des Wassers in einen Stausee einer Bergregion nach einem Sommergewitter in den ersten 12 Stunden, wenn \( x \) die Zeit in \( \mathrm{h} \) und \( f(x) \) die Zuflussgeschwindigkeit in \( \frac{\mathrm{m}^{2}}{\mathrm{~h}} \) ist.
a) Bestimmen Sie den Funktionsterm von \( f \).
b) Berechnen Sie die mittlere Zunahme der Zuflussgeschwindigkeit in den ersten vier Stunden.
c) Bestimmen Sie den Zeitpunkt, an dem die Zuflussgeschwindigkeit am größten war, und geben Sie diese Zuflussgeschwindigkeit an.
d) Begründen Sie mithilfe des Graphen und geeigneter Funktionswerte, dass der Zeitraum, in dem die Zuflussgeschwindigkeit mindestens \( 120 \frac{\mathrm{m}^{2}}{\mathrm{~h}} \) beträgt, länger als 7 Stunden ist.
e) Bestimmen Sie die mittlere Zuflussgeschwindigkeit für die ersten 12 Stunden.
f) Berechnen Sie die Wassermenge, die innerhalb der ersten 2 Stunden zufließt.
g) Bestimmen Sie das zwei Stunden umfassende Zeitintervall, in dem die größte Wassermenge zufließt. Ermitteln Sie dazu einen rechnerischen Ansatz, mit dem das gesuchte Intervall bestimmt werden kann. Beschreiben Sie (kurz) den Lösungsweg. Eine Durchführung der Rechnungen ist nicht erforderlich.