Aufgabe:
Für eine annähemd punktförmige Lichtquelle wird die Intensität \( y \) des Lichts im Abstand \( x \) von der Lichtquelle durch die Funktionsgleichung \( y=\frac{2}{x^{2}} \) beschrieben.
a) Einer der abgebildeten Graphen kann zur Funktionsgleichung \( y=\frac{2}{x^{2}} \) gehören. Kreuzen Sie an.
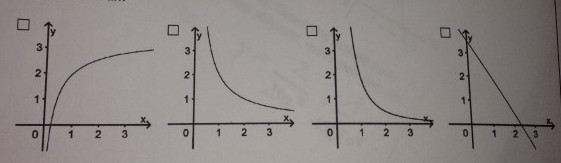
b) Bestimmen Sie die zu \( x=a \) und \( x=5 a \) gehörenden \( y \)-Werte. Geben Sie mithiffe lhrer Ergebnisse an, um wie viel Prozent die Intensität des Lichts abnimmt, wenn man den Abstand zur Lichtquelle verfünffacht.