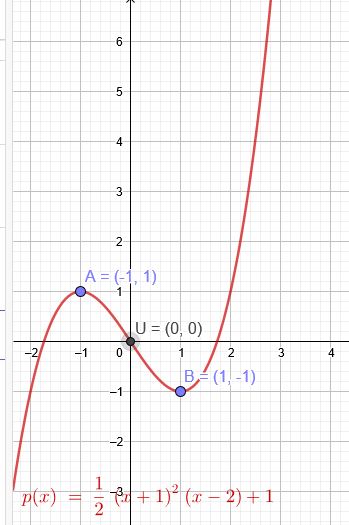
a)
\(A(-1|1)\) \(B(1|-1)\) \(U(0|0)\) liegen auf dem Graphen .
Es liegt eine Symmetrie zum Ursprung vor.
Ich verschiebe den Graphen von f(x) um 1 Einheit nach unten:
\(A´(-\red{1}|0)\) \(B´(1|-2)\) \(U´(0|-1)\)
\(f(x)=a*(x+\red{1})^2*(x-N)\)
\(B´(1|-2)\):
\(f(1)=a*(1+\red{1})^2*(1-N)=4a*(1-N)=-2\)
\(2a*(N-1)=1\) → \(a=\frac{1}{2N-2}\)
\(f(x)=\frac{1}{2N-2}*(x+\red{1})^2*(x-N)\)
\(U´(0|-1)\):
\(f(0)=\frac{1}{2N-2}*(0+\red{1})^2*(0-N)=\frac{1}{2N-2}*(-N)\)
\(\frac{1}{2N-2}*(-N)=-1\)→\(\frac{1}{2N-2}*(N)=1\)→\(N=2\) \(a=\frac{1}{2*2-2}=\frac{1}{2}\)
\(f(x)=\frac{1}{2}*(x+\red{1})^2*(x-2)\)
um 1 Einheit nach oben:
\(p(x)=\frac{1}{2}*(x+\red{1})^2*(x-2)+1\)