Der Graph ist gegeben. Wie lautet die Funktionsgleichung?

Question

(:

Die Frage steht schon in der Überschrift. Ich habe das allerdings nur halb verstanden. Um die Funktionsgleichung zu ermittelnd, braucht man ja m & b, also würde die Gleichung ja mx+b lauten. Nur: Wie bestimmt man m? Um m zu bestimmen, braucht man ja zwei Punkte. Am leichtesten ist das ja, wenn die Gerade zwei Kästchenecken kreuzt. Wie bestimmt man m aber, wenn es kein Kästchen kreuzt? Wie viele Schritte nach oben/unten/seitlich muss man dann gehen, um m zu ermitteln?

Beispiel im Bild (ist zwar schon gegeben, nur noch Erklärung fehlt):

 

Answer 1

"Wie bestimmt man m aber, wenn der Graph kein Kästchen kreuzt?"

Dann versuchst du andere Punkte zu wählen, die ein Kästchen kreuzen. Dazu musst du gegebenenfalls den Graph verlängern. Ansonsten müsstest du die Punktkoordinaten abschätzen, wobei es meist ungenau wird.

Anhand eines Beispiels: f(x) = 1,5*x + 1

Einen Punkt erkennst du bei P₁(0|1), einen weiteren weiter rechts/oben mit P₂(2|4).

Aus diesen beiden Punkten könntest du die Gleichung der linearen Funktion inklusive Steigung ermitteln.

Answer 2

Am besten nimmst du dir zwei Punkte, bei denen du die x- und y-Koordinate genau ablesen kannst (wie weit diese Punkte auseinanderliegen, ist egal). Dann setzt du die Punkte in folgende Gleichung ein, um m zu berechnen:

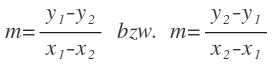
m=\frac { { y }_{ 1 }-{ y }_{ 2 } }{ { x }_{ 1 }-{ x }_{ 2 } } \quad bzw.\quad m=\frac { { y }_{ 2 }-{ y }_{ 1 } }{ { x }_{ 2 }-{ x }_{ 1 } }

Wichtig hierbei ist nur, dass die zugehörigen x und y Werte untereinander stehen. (Ob 1, 2 oder 2, 1, ist egal, da sich dort nur die Vorzeichen im Zähler und Nenner ändern, das Ergebnis bleibt aber dasselbe.)

In deinem Beispiel wurde P1(0|0) und P2(1,5|3) gewählt. Setzen wir das in die Gleichung ein, erhalten wir

(0-3)/(0-1,5)=-3/-1,5=2 bzw. (3-0)/(1,5-0)=3/1,5=2

Falls du noch mehr darüber wissen willst, der Wikipediaartikel ist dazu sehr gut: https://de.wikipedia.org/wiki/Steigung