Bestimmen Sie die Lösungsmenge der Ungleichung: 1/(x-3) ≥ 5/(x+1)

Question

Aufgaben:

3-2.) Bestimmen Sie die Lösungsmenge der Ungleichung

\( \frac{1}{x-3} \geq \frac{5}{x+1} \)

3-3.) Bestimmen Sie die Lösungsmenge der Ungleichung

\( \frac{x-1}{x-2} \geq \frac{x-3}{x-4} \)

Answer 1

2.Fall
16 - 4 x <= 0 und ( x - 1)^2 - 4 < 0

x >= 4 und
( x -1 )^2 < 4
-2 < x -1 < 2
-1 < x < 3
keine Lösung für Fall 2

Lösung 3 < x ≤ 4  bzw. ( x < -1 )

Answer 2

Lösungsmenge der Ungleichung Bsp. 1/(x-3) ≥ 5/(x+1)

1. Methode:

überleg dir den Verlauf der Graphen von

f(x) = 1/(x-3)

und

g(x) = 5/(x+1)

f(x) = 1/(x-3)  ist dasselbe wie h(x) = 1/x aber um 3 Einheiten nach RECHTS verschoben. Vertikale Asymptote von f ist bei x=3. Für x>3 verläuft f(x) oberhalb und für x<3 unterhalb der x-Achse.

und

g(x) = 5/(x+1)  ist dasselbe wie h(x) = 1/x aber um 1 Einheit nach LINKS verschoben. Ausserdem um den Faktor 5 in y-Richtung gestreckt. Vertikale Asymptote von g ist bei x=-1. Für x>-1 verläuft g(x) oberhalb und für x<-1 unterhalb der x-Achse.

Berechne nun noch allfällige Schnittpunkte von f und g.

1/(x-3) = 5/(x+1)         |*Hauptnenner 

x+1 = 5(x-3)

x+1 = 5x - 15

16 = 4x

Einzige Schnittstelle bei x= 4.

Hier https://www.wolframalpha.com/input/?i=+1%2F%28x-3%29+%3D+5%2F%28x%2B1%29+++ siehst du, wie das aussieht

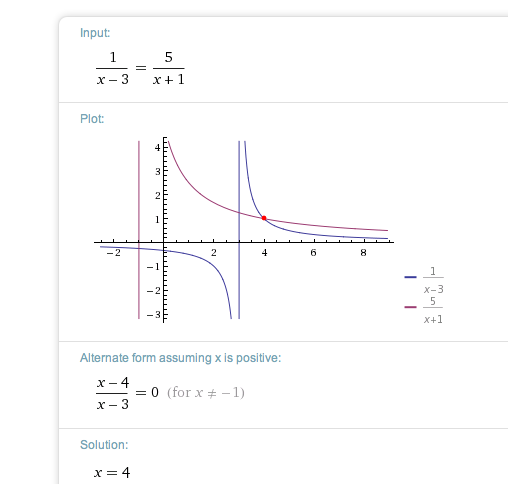
Gesucht ist nun das Gebiet, in dem die blaue Kurve oberhalb der roten verläuft. Du liest das auf der x-Achse ab.

L = ]3, 4] = {x Element R | 3<x≤4}

EDIT: Da man im Koordinatensystem den Teil des roten Graphen links von x=-1 nicht sieht, muss er (aus Symmetriegründen) unterhalb der blauen Kurve verlaufen.

Gesamthaft ergibt sich dann L = {x |  -∞ <x<-1 oder 3<x≤ 4}

Mehr dazu vgl. Diskussion unten.

Comments

Du meinst doch L = ]3,4] oder?

---

Außerdem gilt die Ungleichung auch zum Beispiel für x = -2, also müsste noch eine Fallunterscheidung gemacht werden.

---

Na ja. Es genügt einen Wert im Bereich x<-1 einzusetzen. Wenn sich herausstellt, dass die Ungleichung für x=-2 gilt, so gilt sie für {x| -∞ <x<-1}.

Gesamthaft ergibt sich dann L = {x |  -∞ <x<-1 oder 3<x≤ 4}

Vgl: https://www.wolframalpha.com/input/?i=+1%2F%28x-3%29+≥+5%2F%28x%2B1%29+++

Anmerkung: Wenn man im Koordinatensystem den roten Teil des Graphen links von x=-1 nicht sieht, muss er (aus Symmetriegründen) unterhalb der blauen Kurve verlaufen.

In der Rubrik 'ähnliche Fragen' findest du andere vorgerechnete Beispiele. Lies die mal durch und versuch die 2. Aufgabe mit einer dort gefundenen Methode selbst.

---

@Lu
irgenwie hat dir Wolfram da etwas Falsches gezeichnet.
Die rote Funktion heißt nicht ( links ) x  = -1 sondern geht nach
links weiter.
@Yakyu
siehe meine Antwort

Nachtrag : Irgendwie sind letzter und vorletzter
Kommentar zeitlich verrutscht.

---

georgborn: x=-1 ist vertikale Asymptote an den roten Graphen. Habe ich zu Beginn schon beschrieben. WolframAlpha zeichnet das schon richtig.

---

wähle einmal die Darstellung bis y = -10,
dann sieht der Graph schon anders aus.

---

Ja. Und?

Was in der Lösungsmenge von Wolframalpha stimmt denn nicht?

---

Vielleicht noch zu deiner Frage 3-3

(x-1)/(x-2) ≥ (x-3)/(x-4)             |links und rechts  -1.

(x-1)/(x-2) - (x-2)/(x-2) ≥ (x-3)/(x-4) - (x-4)/(x-4)        |Brüche subtrahieren links und rechts

((x-1)-(x-2))/(x-2) ≥ ((x-3)-(x-4))/(x-4)

1/(x-2) ≥ 1/(x-4)

Jetzt hast du im Prinzip die gleiche Aufgabe vor dir wie bei 3-2.

Versuche das mit deinem Lieblingsverfahren nun noch fertig zu lösen.

f(x) = 1/(x-2) ist h(x) = 1/x um 2 nach rechts verschoben: Vertikale Asymptote bei x=2.

g(x) = 1/(x-4) ist h(x) = 1/x um 4 nach rechts verschoben: Vertikale Asymptote bei x=4. 

Da keiner der Graphen gestreckt ist, gibt es keinen Schnittpunkt. Hier zur Illustration die beiden Graphen.

Im Bereich ]2,4[ zwischen den beiden vertikalen Asymptoten verläuft der Graph von 1/(x-2) oberhalb von Graphen von 1/(x-4)

Daher ist die Lösungsmenge von 3-3 L = {x| 2<x<4}

---

@
Lu meinst du jetzt mich ?

Lu, deine erste Antwort war nicht vollständig

L = ]3, 4] = {x Element R | 3<x≤4}

Wahrscheinlich wegen der nicht ganz optimalen
Darstellung in Wolfram. war dir der andere Lösungs-
bereich nicht aufgefallen.
Diesen hast du erst nachträglich angegeben. EDIT
Darauf hatten dich Yakyu und ich aufmerksam gemacht.

Answer 3

So, hier meine Version. Sie ist ein wenig anders als die anderen Ansätze:

$$ \begin{aligned} \frac { 1 }{ x-3 } &\ge \frac { 5 }{ x+1 } \quad \land \quad x\ne-1 \quad \land \quad x\ne3 \\\\\\ \textrm{1. Fall:}\\\\ \frac { 1 }{ x-3 } &\ge \frac { 5 }{ x+1 } \quad \land \quad \left(x\lt-1 \quad \lor \quad 3\lt x\right) \\\\ x+1 &\ge 5 \cdot x - 15 \quad \land \quad \left(x\lt-1 \quad \lor \quad 3\lt x\right) \\\\ 16 &\ge 4 \cdot x \quad \land \quad \left(x\lt-1 \quad \lor \quad 3\lt x\right) \\\\ 4 &\ge x \quad \land \quad \left(x\lt-1 \quad \lor \quad 3\lt x\right) \\\\ 3 &\lt x \le 4 \quad \lor \quad x \lt -1. \\\\\\ \textrm{2. Fall:}\\\\ \frac { 1 }{ x-3 } &\ge \frac { 5 }{ x+1 } \quad \land \quad \left(-1\lt x \lt 3 \right) \\\\ x+1 &\le 5 \cdot x - 15 \quad \land \quad \left( -1\lt x \lt 3 \right) \\\\ 16 &\le 4 \cdot x \quad \land \quad \left( -1\lt x \lt 3 \right) \\\\ 4 &\le x \quad \land \quad \left( -1\lt x \lt 3 \right) \\\\ x &\in \emptyset. \\\\\\ \textrm{Ergebnis:}\\\\ \frac { 1 }{ x-3 } &\ge \frac { 5 }{ x+1 } \quad \Leftrightarrow \quad 3 \lt x \le 4 \quad \lor \quad x \lt -1. \end{aligned} $$

Comments

super ausführlich ,danke dir