Vektoren im Würfel
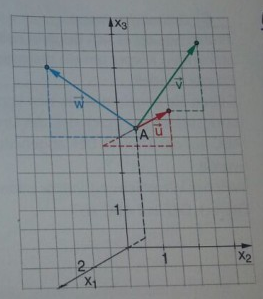
Die Vektoren \( \vec{u}=\left(\begin{array}{l}{2} \\ {2} \\ {1}\end{array}\right), \vec{v}=\left(\begin{array}{c}{-2} \\ {1} \\ {2}\end{array}\right) \) und \( \vec{w}=\left|\begin{array}{c}{1} \\ {-2} \\ {2}\end{array}\right| \) beschreiben mit dem Punkt \( A=(-1|0| 3) \) die Kanten eines Würfels.
a) Bestimmen Sie die restlichen Eckpunkte des Würfels.
b) Wie ändern sich die Eckpunkte, wenn der Würfel um \( \left(\begin{array}{c}{2} \\ {-1} \\ {4} \end{array}\right) \) verschoben wird?
c) Der Würfel wird so verschoben, dass der Punkt A auf den Punkt \( A^{\prime}=(2|4|-4) \) zu liegen kommt. Geben Sie den dazugehörigen Verschiebungsvektor an.