Fläche berechnen mit der Geraden x=z .............

Question

gegeben: $$ f^{ t }\left( x \right) =t-\frac { 4 }{ x² } $$    ; t>0   $$ x\neq 0 $$

Ihr Schaubild ist Kt(t im index)

Aufgabe: Die Gerade x=z schneidet Kt im ersten Feld. SIe schließt mit Kt, den beiden Achsen und der geraden y=t eine Fläche mit dem Inhalt At(z) ein.

Berechnen Sie At(z) und den $$ lim\xrightarrow { z\rightarrow \infty  } At(z) $$.

Ich bitte um Hilfe

Answer 1

f ( x ) = 4 - t / x^2

Schnittpunkt von  y = t und f

f ( x ) = t
4 - t / x^2 = t
t / x^2 = 4 - t
x^2 = t / ( 4 - t )
x = √ [ t / ( 4 - t ) ]

Den Schnittpunkt nenne ich jetzt m.
( Siehe Skizze )

∫ f ( x ) dx
∫ 4 - t / x^2 dx
4x + ( 2 * t ) / x^3
Integrationsgrenzen m .. z
[ 4x + ( 2 * t ) / x^3 ]_m^z
hinzuaddiert werden muß noch die Fläche m * t

Gleich gehts weiter

Comments

lim z -> ∞ [ A_t ( z ) ] = 4z + ( 2 * t ) / z³ - ( 4m + ( 2 * t ) / m³ ) + m*z
Der erste Summand 4z geht gegen unendlich
der 2.Summand ( 2 * t ) / z³ geht gegen null
- ( 4m + ( 2 * t ) / m³ )  dies ergibt einen Wert
der letzte Summand + m*z geht gegen unendlich
Insgesamt gegen unendlich

---

danke für die schnelle Antwort, aber die Funktion lautet $$ f\left( x \right) =t-\frac { 4 }{ x² } $$

und nicht f(x)=4 - t / x²

^{ich hoffe sie können mir weiterhelfen}

---

Korrektur

f ( x ) = t - 4 / x²

Schnittpunkt von  f mit der x-Achse
t - 4 / x² = 0
4 / x^2 = t
x^2 = 4 / t
x = √ ( 4 / t )

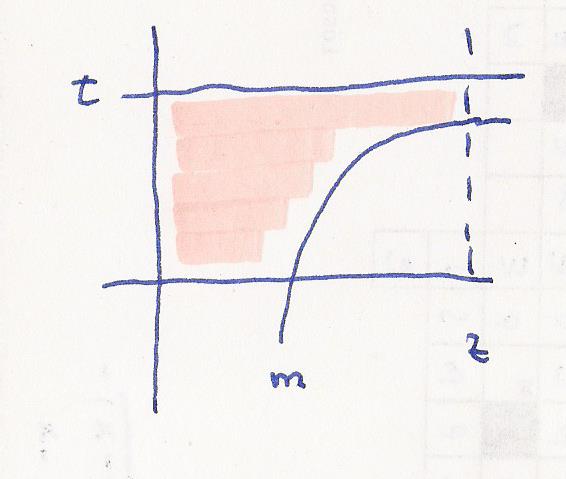
Den Schnittpunkt nenne ich jetzt m.
m = √ ( 4 / t )

Der linke Teil der Fläche ist das Rechteck
m * t

Stammfunktion von f
∫ t - 4 / x² dx
t * x + 4 / x

Rechter Teil der Fläche
das Rechteck t * ( z - m )
- die Fläche unterhalb der Kurve
 [  t * x + 4 / x ]_m^z

A ( x ) = m * t +  t * ( z - m ) - [  t * x + 4 / x ]_m^z
A ( x ) = m * t +  t z - tm  - [  t * z + 4 / z  - (  t * m + 4 / m ) ]
A ( x ) =   t z   - [  t * z + 4 / z  - t * m - 4 / m ) ]
A ( x ) =   t z   - t*z - 4 / z  +  t m + 4 / m 
A ( x ) =   tm  - 4 / z  + 4 / m
( für m gilt : m = √ ( 4 / t ) siehe oben  )

lim z -> ∞ [ tm  - 4 / z  + 4 / m]
( 4 / z geht gegen 0 )
lim z -> ∞ [ tm + 4/m ]

So. Müßte alles stimmen.

---

sie die Integrationsgrenzen ihrer markierten Fläche nicht 0 und Z ?

---

Vorbemerkung : hier im Forum wird meist das " du " gebraucht.

Die Fläche geht von 0 bis z.
Der linke Teil von x = 0 bis x = m ist das Rechteck m * t.

Die Kurvenfläche beginnt beim Schnittpunkt der Kurve mit der
x-Achse bei x = m und geht bis x = z.

Es wird die Differenzfunktion zwischen der Geraden y = t
und f ( x ) gebildet und diese integriert.

mfg Georg