nach Information durch eh659
a. die langfristige Preisuntergrenze (=Preis zum Grenzbetrieb)
K ( x ) = E ( x ) = p ( x ) * x
x = 17 Stück
K ( x ) = 2.471 €
Preis ( x ) = 149.83 €
Erlös ( x ) = 2.547 €
Ab 17 Stück wird Gewinn gemacht.
Ab 360 Stück wird dann wieder Verlust gemacht.
( siehe erste Antwort )
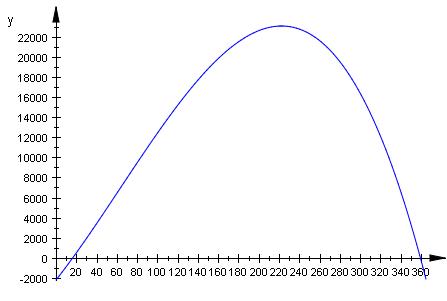
b. die Gewinnzone, den maximalen Gewinn und die
Koordinaten des Cournot´schen Punktes.
Die Gewinnzone liegt zwischen 17 Stück und 360 Stück.
Die Gewinnfunktion ist
G ( x ) = E ( x ) - K ( x )
G ( x ) = p ( x ) * x - K ( x )
G ( x ) = ( 150 - 0.01 * x ) * x - 0.002 * x^3 - 0.39 * x^2 + 22 * x + 2200
Der maximale Gewinn ist der Extrempunkt ( 1.Ableitung = 0 )
G ´( x ) = 0
[ 150 * x - 0.01 * x^2 - 0.002 * x^3 - 0.39 * x^2 + 22 * x + 2200 ] ´ = 0
150 - 0.02 * x - 0.006 * x^2 - 0.78 * x + 22 = 0
x = 223 Stück
G ( 223 ) = 23062 €
Cournotsche Punkt
( 223 | 23062 )
zum Punkt siehe
https://de.wikipedia.org/wiki/Cournotscher_Punkt
c) Kostenkehre = Wendepunkt von K(x)
( siehe Link eh659 )
K ´´ ( x ) = 0
K ( x ) = 0.002 * x^3 - 0.39 * x^2 + 22 * x + 2200
K ´ ( x ) = 0.006 * x^2 - 0.78 * x + 22
K ´´ ( x ) = 0.012 * x - 0.78
0.012 * x - 0.78 = 0
0.012 * x = 0.78
x = 65