Berechnen Sie die Länge des Schachtes

Question

1. In eine Pyramide mit der Grundkante a=90m und der Höhe h=60m führen zwei Schächte. Ein Schacht verläuft vom Punkt P(69|49|28) aus in Richtung u⃗ =⎛⎝⎜−20−1⎞⎠⎟, ein zweiter vom Punkt Q(50|81|12) aus in Richtung v⃗ =⎛⎝⎜0−5−1⎞⎠⎟(Angaben in Meter).
   Die beiden Schächte sollen durch einen möglichst kurzen Schacht verbunden werden. Berechnen Sie, in welchen Punkten der vorhandenen Schächte die Bohrung beginnen bzw. enden muss. Berechnen Sie die Länge des Schachtes.

⎛⎝
⎛⎝

Comments

Beim ersten Richtungsvektor fehlt sicher etwas

[69, 49, 28] + r·[x, -20, -1] ??

[50, 81, 12] + s·[0, -5, -1]

Bitte einmal die Punkte und Richtungsvektoren prüfen und vervollständigen.

---

[69, 49, 28] + r·[ -2,0, -1] 

[50, 81, 12] + s·[0, -5, -1]

---

Die Geradengleichungen lauten:

g: [69, 49, 28] + r·[-2, 0, -1]

h: [50, 81, 12] + s·[0, -5, -1]

Der Normalenvektor

N = [-2, 0, -1] ⨯ [0, -5, -1] = - [5, 2, -10]

Nun stellen wir uns das mal vor 

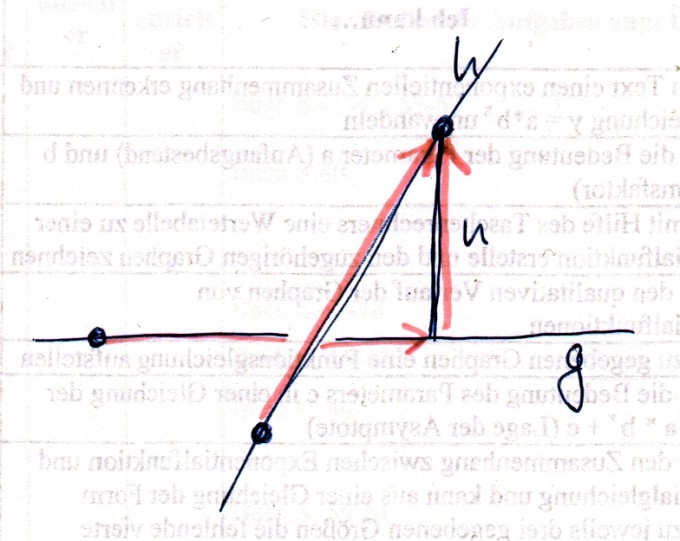
Es gibt nun 2 Möglichkeiten zum hinteren Punkt der oberen Geraden zu kommen. Die setzen wir gleich

[69, 49, 28] + r·[-2, 0, -1] + n·[5, 2, -10] = [50, 81, 12] + s·[0, -5, -1]

Das ist ein LGS mit 3 Gleichungen und 3 Unbekannten. Das lösen wir.

n = 1 ∧ s = 6 ∧ r = 12

Die Schachtenden berechnen wir indem wir in unsere Geradengleichungen r und s einsetzen. Die Schachtlänge indem wir von der Verbindungsstrecke die länge nehmen

[69, 49, 28] + 12·[-2, 0, -1] = [45, 49, 16]

[50, 81, 12] + 6·[0, -5, -1] = [50, 51, 6]

|1·[5, 2, -10]| = √129 = 11.36

Answer 1

Die Ausführungen im Kommentar genügen eigentlich als Antwort. Ich wollte zunächst ja gar nicht so viel in den Kommentar schreiben. Ist dann aber doch mehr geworden.