Nullstellen von ln(2x)+x^2 mit dem Newtonverfahren

Question

brauche mal eure Hilfe.

Ich soll die Nullstellen der Funktion y=f(x)=ln(2x)+x² per Newton'schem Iterationsverfahren herausfinden.

Das Verfahren habe ich vor mir liegen, aber leider sind alle Beispiele nur mit normalen Funktionen.

 

Nun stört mich das ln(2x). Kann ich daraus nicht einfach f(x)=e^{x^2}+2x machen? Aber dann hätte ich keine Nullstelle....

Könnt ihr mir helfen, wie ich das umformen kann?

Answer 1

Es ist doch eigentlich egal was du für eine Funktion hast. Du brauchst einfach nur die Ableitung bilden:

f(x) = LN(2·x) + x^2

f '(x) = 2·x + 1/x

Nun stellen wir die Iterationsvorschrift auf. Ich lasse mal das n und n+1 weg.

x = x - (LN(2·x) + x^2) / (2·x + 1/x)

Nun setzt man rechts die erste Wermutung ein und erhält dann die nächste Näherung. Ich fange mal mit 1 an.

1
0.4356176064
0.4192228311
0.4193648124
0.4193648240
0.4193648240

Da sich der Wert jetzt nicht mehr ändert nehme ich das als Wert für die Nullstelle.

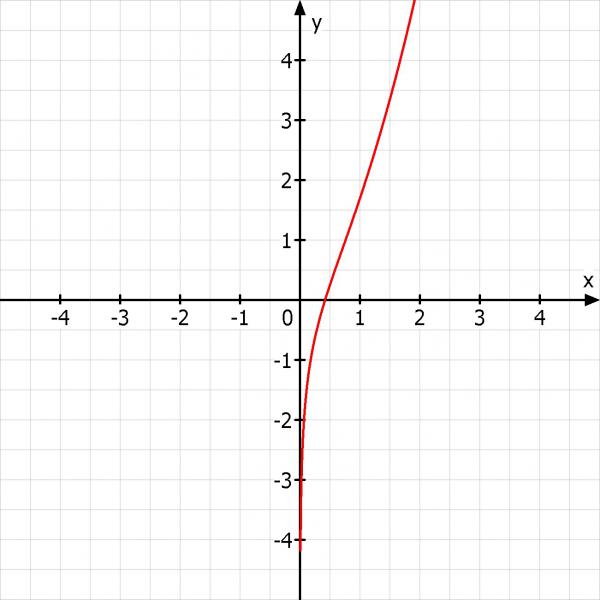
Ich kann den Graphen noch mal skizzieren