Berechne die zu überbrückende Entfernung, wenn der Ball genau von einer Uferstelle zur anderen fliegt. + Wendestellen

Question

Aufgabenstellung:

Nach dem grandiosen zweiten Platz der MCG Mannschaft bei Golt Turnier von Jugend trainiert für Olympia, er wägt das MCG im Zuge des Neubaus auch einen Golfplatz zu erwerben. Dazu wurde ein idyllisch liegender Golfplatz am Rande von Hamburg gefunden. Der Platz ist durch einen See zweigeteilt, wie in der Skizze zu erkennen.

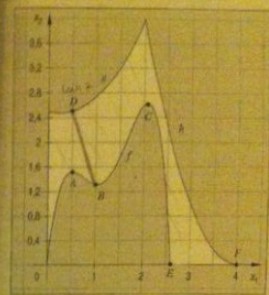
Der inselartig geformte Teil wird durch ein Ufer begrenzt, dessen Uferlinie der Funktion \( f(x)=-2 x^{4}+\frac{28}{3} x^{3}-14 x^{2}+8 x \) entspricht.

Der Hauptteil des Golfplatzes liegt nördlich auf dem Festland, seine Uferlinie ist durch die Funktionen \( g(x)=0.5 x^{2}-0.25 x+2,5: 0 \leq x \leq 2 \) und \( h(x)=x^{2}-8 x+16 ; \quad 2 \leq x \leq 4 \) gekennzeichnet.

Eine Einheit entspricht 100 Metern.

a) In der Nähe des Punktes B auf der Insel befindet sich der Abschlag für das Loch 7 (Punkt D), das auf dem Festland genau nördlich vom Punkt A liegt. Berechne die mit einem Schlag zu überbrückende Entfernung, wenn man davon ausgeht, dass der Ball genau von einer Uferstelle zur anderen fliegt.

b) Für eine TV-Übertragung des ersten MCG - Open soll eine bewegliche Kamera an einem Kabel befestigt werden, das die beiden Punkte A und C verbindet, so dass die sportlichen Höchstleistungen der MCG'ler auf der Insel besser in Szene gesetzt werden können. Ermittle die Länge des Kabels.

c) Berechne die Wendestellen.

d) Als weitere Möglichkeit zur Seeüberquerung erwägt die erweiterte Schulleitung den Bau einer Fußgängerbrücke, die an der kürzesten Entfernung zwischen der Insel und dem nordwestlichen Teil des Festlands in nördlicher Richtung gebaut werden soll. Ermittle die Stelle für diese Brücke und ihre Länge.

e) Bestimme die Entfernung der Punkte \( \mathrm{E} \) und \( \mathrm{F} \).

Lösungsansätze:

bei a) habe ich den Extrempunkt von f(x)  bei (0,25 | 2,47)  und für g(x) bei (1| 4/3), jedoch weiß ich nicht wie man dann die Entfernung dieser Punkte berechnet oder abliest.

bei b) habe ich überlegt das Integral mit den Punkten A und C in der Graphik als Grenzen zu berechnen, weiß aber nicht, wie das dann mit der Länge des "Kabels", also dem Graphen in diesem Abschnitt zusammenhängt.

Answer 1

a) In der Nähe des Punktes B auf der Insel befindet sich der Abschlag für das Loch 7 (Punkt D), das auf dem Festland genau nördlich vom Punkt A liegt. Berechne die mit einem Schlag zu überbrückende Entfernung, wenn man davon ausgeht, dass der Ball genau von einer Uferstelle zur anderen fliegt.

B = [1, f(1)] = [1, 4/3]

D = [1/2, f(1/2)] = [1/2, 5/2]

|BD| = √((1 - 1/2)^2 + (4/3 - 5/2)^2) = 1.269295517 → 127.9 m

b) Für eine TV-Übertragung des ersten MCG-Open soll eine bewegliche Kamera an einem Kabel befestigt werden, das die beiden Punkte A und C verbindet, so dass die sportlichen Höchstleistungen der MCG'ler auf der Insel besser in Szene gesetzt werden können. Ermittle die Länge des Kabels.

A = [0.5, f(0.5)] = [0.5, 37/24]

C = [2, f(2)] = [2, 8/3]

|AC| = √((0.5 - 2)^2 + (37/24 - 8/3)^2) = 1.875 → 187.5 m

zu c) Wendestellen

f(x) = - 2·x^4 + 28/3·x^3 - 14·x^2 + 8·x

f'(x) = - 8·x^3 + 28·x^2 - 28·x + 8

f''(x) = - 24·x^2 + 56·x - 28 = 0

x = 7/6 ± √7/6

x = 0.7257081148 ∨ x = 1.607625218

f(0.72571) = 1.445

f(1.6076) = 2.098

Comments

Wie sind Sie bei b) auf die Koordinaten der Punkte gekommen, durch Errechnen der Extrema der Funktion f(x)?

Wieso sind die 7/6 unter der Wurzel nicht quadriert, ergibt dieses "p/2² - q " unter der Wurzel der pq-Formel zusammengefasst 7/6?

---

Nein. Es steht ja nicht das A und C die Extrema der Funktion sein sollen. Daher habe ich einfach x Werte angenommen und die Y-Werte berechnet.

Die 6 ist nicht mehr unter der Wurzel. Das ist schon vereinfacht.

Answer 2

zu c) Wendestellen

f(x) = -2x⁴ + 28/3x³ - 14x² +8x
f'(x) = -8x³ + 28x² - 28x + 8
f''(x) = -24x² + 56x - 28

f''(x) = -24x² + 56x - 28 = 0 | : (-24)
x² - 7/3 * x + 7/6 = 0

pq-Formel
x_1,2 = 7/6 ± √(49/36 - 42/36) = 7/6 ± √(7/36)
x₁ ≈ 1,6076
x₂ ≈ 0,7257

Probe:
-24*1,6076² + 56*1,6076 - 28 = 0,00053376 ≈ 0
-24*0,7257² + 56*0,7257 - 28 = -0,00017176 ≈ 0

Diese Werte in die Funktionsgleichungen eingesetzt sollte die Wendepunkte ergeben.
(Deine Graphik scheint meine Ergebnisse zu bestätigen.)

Besten Gruß

Answer 3

Gegebenheiten ( jedenfalls was ich herauslese )
Gesucht ist die kürzeste Entfernung zwischen zwischen f und g
als senkrechte Gerade.
Da ich die Formel im Detail nicht so gut sehen kann.

g ( x ) - f ( x ) ist die Entfernung.
Von der Funktion die 1.Ableitung bilden und die Extremwerte
feststellen. Dann noch schauen was min bzw. max ist.

Comments

f(x) = - 2x⁴ + 28/3 x³ - 14x² + 8x  ist der untere Graph

g(x) = 0,5x² -0,25x + 2,5   ist der obere
     hier steht noch dabei: 0 < x < 2

---

1.Antwort :

g ( x ) ist der obere Graph. f ( x ) ist der unter Graph.
Also hat die Differenzfunktion  schon einmal das " richtige "
Vorzeichen.

In der Aufgabenstellung steht  ( man merkt hier den maritimen
Einfluß ) " die kürzeste Entfernung zwischen der Insel  und dem
nordwestlichen Teil. Norden ist oben, nordwestlich ist g ( x )
wie definiert zwischen 0 und 2.

Die Brücke soll in nördlicher Richtung gebaut werden. Also
senkrecht nach oben.

---

Die Differenzfunktion ist
d ( x ) = g ( x ) - f ( x )
d ( x ) = 2x^4 - 28/3 * x^3 + 14.5 * x^2 - 8.25 * x + 2.5
d ´( x ) = 8x^3 - 28x^2 + 29x - 8.25

Eine Extremwert läßt sich nur mit Hilfe z.B.
des Newton-Verfahrens berechnen.

Die Extremwerte sind
x = 0.47 Abstand 0.95
x = 1.21 Abstand 1.50
x = 1.82 Abstand 1.19

Bei x = 0.47 ist die kürzeste Entfernung.

Das Newton-Verfahren habt ihr sicher noch
nicht gehabt.
Ich könnte mir vorstellen das ihr die Lösung
einfach durch Ausmessung an der Skizze
finden sollt.