Hi Linda,
probieren wir es nochmal :-)
Es gibt 3 binomische Formeln:
1. (a + b)2 = a2 + 2ab + b2
2. (a - b)2 = a2 - 2ab + b2
3. (a + b) * (a - b) = a2 - b2
In diesem Zusammenhang sind für uns nur die ersten beiden interessant.
Du könntest natürlich zum Beispiel auch schreiben
(x + y)2 = x2 + 2xy + y2
um Dir das klarer zu machen; die Verwendung von a und b ist aber üblich.
Bei der quadratischen Ergänzung geht es darum, das letzte Summenglied (also das y2) so zu ergänzen, dass wir auf eben eine dieser binomischen Formeln kommen.
Wir haben gegeben
x2 - 6x
Wir müssen also - wegen des Minuszeichens - irgendwie auf die 2. binomische Formel kommen:
(x - y)2 = x2 - 2xy + y2
Also
-6x = - 2xy | * (-1)
6x = 2xy | : x
6 = 2y | : 2
y = 3
Und dies müssen wir quadrieren, um auf y2 zu kommen, also
y2 = 32 = 9
Das ist unsere quadratische Ergänzung!
Wir kommen also auf
x2 - 6x + 9 = (x - 3)2
Nun haben wir aber 9 hinzuaddiert, müssen es also, um den Ausdruck nicht zu verändern, auch wieder subtrahieren:
x2 - 6x + 9 - 9 = (x - 3)2 - 9
Warum macht man das Ganze?
Mit dieser Scheitelpunktform sieht man sofort, wie der Graph aussieht:
Es ist die Normalparabel, um 3 nach rechts und um 9 nach unten verschoben:
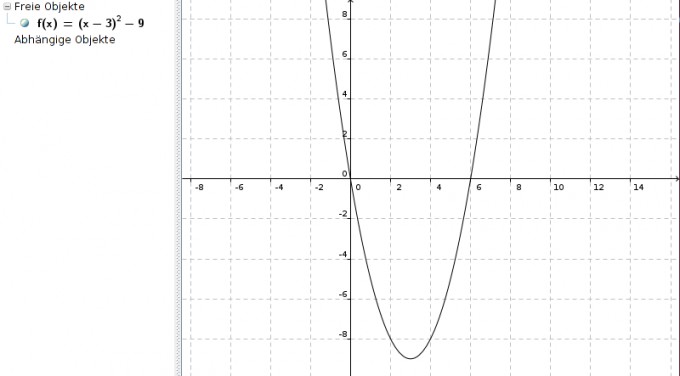
und dies entspricht eben genau der ursprünglichen Funktion f(x) = x2 - 6x:
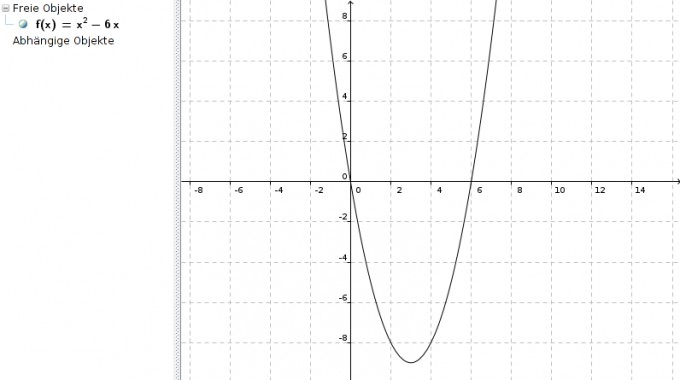
Ich hoffe, dass es jetzt ein wenig deutlicher geworden ist :-)
Besten Gruß