Brückenbogen über Alster. Nenne die Funktionsgleichung, die den Verlauf der Parabel beschreibt. (Quadratische Funktion)

Question

Aufgabe Alsterschifffahrt:

Auf der Alster soll eine neue Fahrroute eingerichtet werden. Dabei müssen die Schiffe unter Brücken hindurchfahren. Die Brückenbögen haben die Form einer Parabel. Die Höhe in der Mitte beträgt \( 2 \mathrm{~m} \).

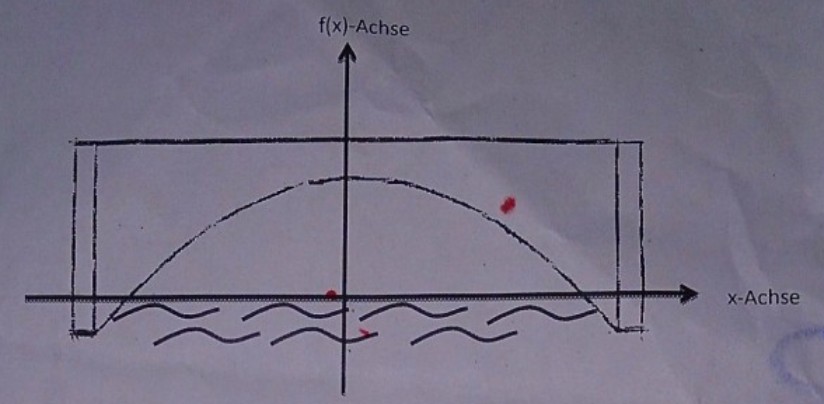
Der Graph ist in einer Skizze dargestellt.

a) Nenne die Funktionsgleichung, welche den Verlauf der Parabel beschreibt. Zur Auswahl stehen:

\( f(x)=\frac{1}{2} x^{2}+2 \quad f(x)=-\frac{1}{2} x^{2}+2 \quad f(x)=\frac{1}{2} x^{2}-2 \)

b) Die allgemeine Form einer quadratischen Funktion lautet \( f(x)=a \cdot x^{2}+b \cdot x+c \). Nenne die Werte für \( a, b, c \) für deine gewählte Funktionsgleichung aus Aufgabe a).

c) Begründe: Warum beschreibt die Funktion den Verlauf?

d) An welchen Stellen trifft die Brücke auf die Wasseroberfläche?

e) Fertige eine Zeichnung zu der Funktion an. Wähle dazu eine geeignete Achsen-Einteilung.

f) Kann ein Schiff mit einer Breite von \( 4 \mathrm{~m} \) und einer Höhe von \( 2 \mathrm{~m} \) über der Wasseroberfläche unter dieser Brücke durchfahren?

Answer 1

b) a = - 1/2 ; b = 0 ; c = 2

c) Man hat eine nach unten geöffnete Parabel daher muss a < 0 sein. Wir haben einen positiven y-Achsenabschnittm daher muss c > 0 sein. Der Scheitelpunkt ist auf der y-Achse daher muss b = 0 sein.

d) f(x) = 0 --> x = -2 ∨ x = 2

e) Niemals. Die Spannweite in Höhe des Wasserspiegels ist ja gerade 4 m. Dann durfte das Schiff nur eine Höhe von 0 haben.

Answer 2

a hast du schonmal richtig ausgewählt, das ist die richtige

b)

die funktion drüber könnt eman auch so hinschreiben:

f(x)= -1/2x^2 +0x +2

villeichst siehst du es so besser

a= -1/2

b= 0

c= 2

c) begründe warum beschreibt die Funktion den Verlauf.

-a weil die Parabel nach unten geöffnet ist +2 weil sie auf der y-achse nach oben verschoben ist

d) ist die Nullstellenberechnung

Ich hab das mit der Mitternachtsformel/a-b-c-Formel gelernt. Siehe https://www.matheretter.de/wiki/abc-formel

e) ist selbsterklärend

f) x2-x1 = die breite der Brücke die höhe ist der Wert C

Wär schön wenn du das nächste mal hinschreibst was du bisher geschafft hast, nur das Blatt zu fotografieren ist auch nicht sinn der sache, du willst ja nicht nur die lösungen wissen, sondern auch selber lernen und verstehen wie man darauf kommt.