Hi,
Ableitung:
ableiten kannst Du, oder?
Du kannst hier summandenweise ableiten also einfach die Potenzregel anwenden ;)
Merke dir: 1/an = a-n, also 1/x2 kann man schreiben als x-2 und das jetzt ableiten und x wird beim ableiten 1
f'(x)= -2x-3+1 kann man auch schreiben als -2/x3+1
also lautet deine Ableitung f'(x)=-2/x3+1
Tangentengleichung:
Du weißt, wie eine Geradengleichung aussieht? (Eine Tangente ist ja eine Gerade) y=mx+b, wobei m die Steigung und b der y-Achsenabschnitt ist.
Du hast auch einen Punkt, dieser lautet P(1|2) Du setzt jetzt einfach dein x=1 aus dem Punkt für x in die 1.Ableitung ein, also
f'(1)= -2/13+1 = -1
Also weitß Du, dass deine Tangente schonal so aussieht: y=-x+b
Jetzt setzt Du noch dein x und y-Wer aus dem Punkt P(1|2) in y=-x+b ein und stellst die Gleichung nach b um:
2=-1+b |+1
3=b
Also lautet deine Tangentengleichung: y=-x+3
Hier nochmal das ganze als eine Skizze:
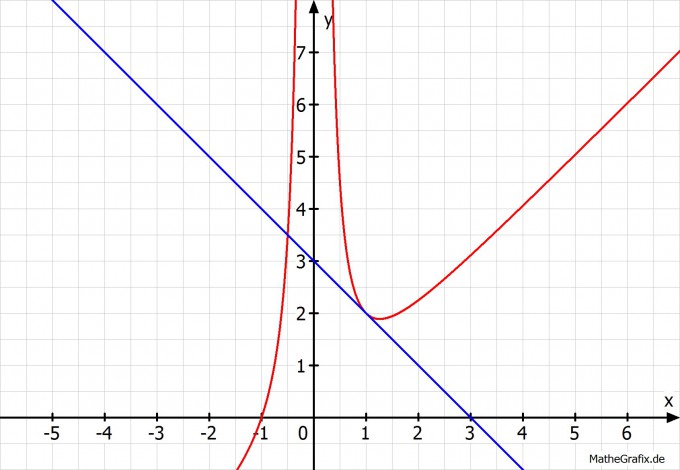
Alles klar soweit?!
Falls noch fragen sind, einfach kommetieren :)
Gruß