Hier noch als Ergänzung zu Akeleis Rechnung die allgemeine Lösung - alle gesuchten Größen in Abhängigkeit der bekannten Größen. Die Lösungen findest du auch hier: Pyramide online berechnen.
G - Grundfläche // das ist hier die Fläche des Quadrats
M - Mantel // das ist die Summe der Fläche der vier Dreiecke
O - Oberfläche // das ist die Summe aus Mantel und Grundfläche
a - Grundseite // Grundseite, alle vier Seiten sind gleichlang da die Grundfläche ein Quadrat ist
hs- Höhe auf a // ist die Höhe im Seitendreieck auf die Grundseite;
ist in jedem der vier Dreiecke gleich, wenn h auf dem Schwerpunkt des Quadrates steht
h - Höhe // Höhe der Pyramide
V - Volumen // das Volumen der Pyramide
FD // Fläche eines der vier Dreiecke, die die Pyramide bilden
FΔ- Dreiecksfläche (allgemein, nicht speziell auf die Pyramide bezogen)
gΔ- Grundseite eines Dreiecks
hΔ- Höhe auf die Grundseite gΔ des allgemeinen Dreiecks
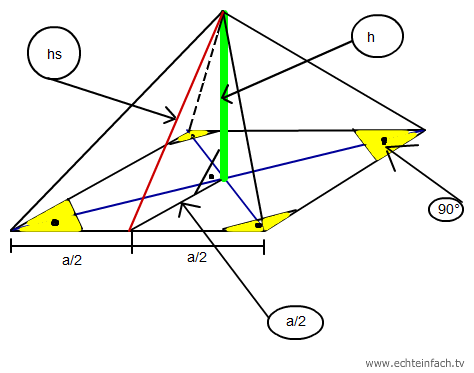
Skizze: Quadratische Paramide (Ecken mit Punkt: rechte Winkel; grün: Höhe der Pyramide; rot: hs)
Grundlegende Gleichungen:
Volumen einer Pyramide:
[1] V = 1/3 * h * G
Oberfläche einer Paramide:
[2] O = M + G
Fläche eines Dreiecks:
[3] FΔ = 1/2 * gΔ * hΔ
Satz des Pythagoras:
[4] u^2 + v^2 = w^2
Gegeben, damit bekannt:
O = 39,2 cm // bekannte Größen sind durch Fettdruck gekennzeichnet
a = 3,0 cm
Berechnungen:
Berechnung von hs:
G = a^2
M = O - G = O - a^2 // siehe [2]
M = 4 * FD // alle vier Dreiecksfläcnen zusammen ergeben die Mantelfläche
FD= M / 4
FD= hs * a/2 // siehe [3]; ausführlicher: FD= 2 * ( 1/2 * hs * a/2)
M / 4 = hs * a/2
hs= M / (2a) = (O - a^2) / (2 * a)
Berechnung von h:
h2s = (a/2)2 + h^2 // siehe [4]
h = sqrt( h2s - (a/2)2 )
h = sqrt( ( (O - a^2)/(2a) )^2 - a^2/4 )
Berechnung von V:
V = a^2/3 * sqrt( ( (O - a^2)/(2a) )^2 - a^2/4 ) // siehe [1]