Bilde dir mal die 5 Ableitungen, Du weißt denke ich wieso 5, oder?
f(x)= (e2x-1)/x
f'(x)= ((e2x(2x-1)+1)/x2
f''(x)= (2(e2x(2x2-2x+1)-1)/x3
Ab hier habe ich mich leider verrechnet. Ich denke die Ableitungen kannst Du aber bilden?
Nun schreibst Du die Formel der Taylorentwicklung auf, diese lautet:
f(x)≈f(x0)+f'(x0)/1+f''(x0)/2!(x-x0)2+f'''(x0)/3!(x-x0)3+f''''(x0)/4!(x-x0)4+f''''(x0)/5!(x-x0)5
So du weißt dein x0=0 ist und kannst es sofort einsetzen:
f(x)≈f(0)+f'(0)/1+f''(0)/2(x-0)2+f'''(0)/3!(x-0)3+f''''(0)/4!(x-0)4+f(5)(0)/5!(x-0)5
So nun kannst Du alles in die Ableitung einsetzen und ausrechnen mit dem TR. Das kannst du selber machen. Das ist mir zuuu anstrengend ^^
Und dann einfach nach der Formel arbeiten...
Am Ende solltest du auf:
T(x)≈2+2x+4x2/3+2x3/3+4x4/15+4x5/45
Am Ende solltest das ganze so aussehen:
f(x)= e2x-1/x
T(x)≈ 2+2x+4x2/3+2x3/3+4x4/15+4x5/45
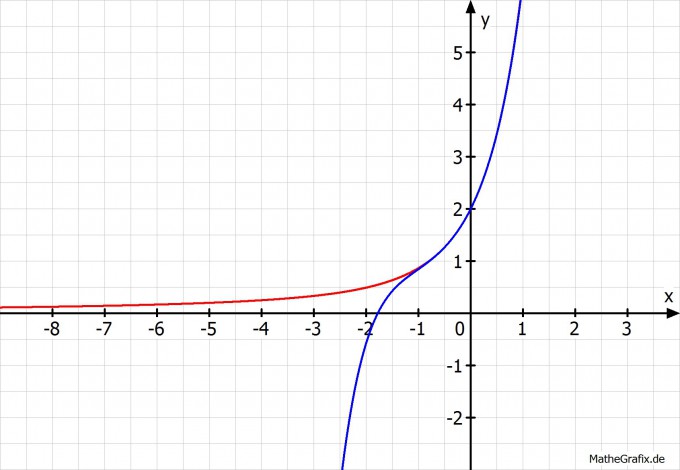
PS: Ich hatte sowas noch nie in der Schule. Noch nicht mal die Differentialrechnung. Deshalb Angaben ohne Gewähr!