Länge einer Ellipse berechnen nur mit Breite und Länge?

Question

wenn man eine Ellipse hat, welche sich in einem Rechteck befindet und dieses maximal ausfüllt, kann man dann die Länge der Ellipse berechnen über die Breite und Länge des Rechteckes?

Den Flächeninhalt habe ich schon:  Breite*Länge*(π/4)

Ich habe bisher nichts gefunden.

Comments

Ich finde bei der finnischen Version von Wikipedia eine Formel für den Ellipsenumfang ('die Ellipsenlänge'). 

http://fi.wikipedia.org/wiki/Ellipsi

Ellipsin kehän pituutta p = 4a* Integral √(1 - e^2 sin^2 t) dt von 0 bis π/2.

Das Epsilon ist die Exzentrizität der Ellipse.

Schalte die Sprache von Wikipedia irgendwohin um, wo die Formel auch steht und du die Sprache verstehst. 

In der deutschen Version siehe hier: https://de.wikipedia.org/wiki/Ellipse#Umfang

---

Danke für die Mühe, aber ich glaube ich suche wohl das falsche, wenn es schon in Richtung Integralberechnung mit Sinus geht. Trotzdem danke! War ein Versuch wert.

Answer 1

Was verstehst du unter Länge der Ellipse ?

vielleicht findest du hier was  dazu:

http://www.mathematische-basteleien.de/ellipse.htm

Comments

Schon okay, scheint so, als ob diese Frage nicht so zu beantworten wäre. Einen Kreis kann man durch seinen Durchmesser beschreiben, ein Rechteck durch seine Diagonale. ich dachte sowas gäbe es auch bei der Ellipse

---

Mit einer einzigen Angabe kann man fast gar nichts beschreiben. Mit der Länge der Diagonale lassen sich  unendlich viele Rechtecke beschreiben - nur mal so als Beispiel ...
Je differenzierter die Eigenschaften des Objekts sind, umso mehr Angaben müssen zur Verfügung stehen. Idealerweise hält man sich bei der Benennung an die üblichen Bezeichnungen.

Answer 2

Dargestellt ist eine 1/4 Ellipse.

Das einbeschriebene Rechteck ist von der Fläche das größtmögliche.

Es ergibt sich :
a = √2  * x
b = √2  * y

Der Umfang ist ( laut Wikipedia )

U ≈ π * ( a + b ) ( Näherung )

Answer 3

Bonsoir,

wie üblich bin ich zu spät, aber dennoch...

unter der Länge einer Ellipse verstehst Du sicherlich auch die beiden am weitesten vom Mittelpunkt entfernten Ellipsenpunkte bzw. die beiden am nächsten liegenden (also die großen und kleinen Halbachsen).

Und ja klar...Du kannst aus gegebener Länge und Breite eines Rechtecks die Länge einer Ellipse errechnen.

(Im Astronomieunterricht ist das an der Tagesordnung).

Meine aus Zeitgründen nur über den Daumen gepeilte, alles andere als maßstabsgerechte Graphik mag Dir dabei ein wenig helfen...die Ellipsenform zu ummalen überlasse ich aber Dir !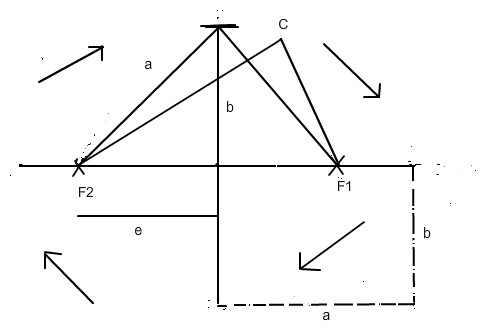 

Hierbei gilt:

a² = e² + b²

sowie die Strecke F2C + Strecke CF1 = 2a

(Falls Du die Ellipse jetzt noch zeichnen möchtest: Befestige 2 Reißnägel in F1 und F2 und spanne eine Schnur mit der Länge 2a um die Nägel. Mit einem "Schreibpflock" kannst Du nun den Weg der Ellipse nachziehen.)

Das müsste Dir eigentlich ein wenig helfen !

Bonne nuit

Sophie

Comments

Hallo Sophie,
dieser Kommentar hat nichts mit der Aufgabe zu tun.
Wir hatten vor ein paar Tagen das Thema Probe durchführen.
Ich schreibe meinen Standardtext dazu bei entsprechenden
Fragen. Du fandest den Kommentar etwas spöttisch.

Hier ein Beispiel von jemandem der ganz anders empfunden
hat

https://www.mathelounge.de/176248/lineare-funktion-schnittpunkt-berechnen

Ist aber alles nichts dramatisches.

---

Lieber Georg,

ich hatte Deinen besagten Kommentar noch gar nicht gelesen, pardon.

Prinzipiell ist es natürlich richtig, was Du sagst, aber trotzdem mag ich es, wenn man auch noch einen Blick über meine Rechenwege wirft, da ich diesbezüglich manchmal zu ziemlichen Kapriolen neige.

Sophie

P.S. Dramatisch ?...keine Spur, solange ich darüber lachen kann :)