Aufgabe:
Eine Firma baut Sprungschanzen für BMX-Fahrer in verschiedenen Formen, deren seitliches Profil jeweils durch den Graphen einer Funktion \( f_{e} \) mit der Gleichung
$$ f_{a}(x)=-\frac{1}{4 \cdot a^{2}} x^{3}+\frac{3}{4} x, \quad-8 \leq x \leq 0 $$
beschrieben wird mit \( 3,2 \leq a \leq 4\left(x, a\right. \) und \( f_{a}(x) \) in Metern).
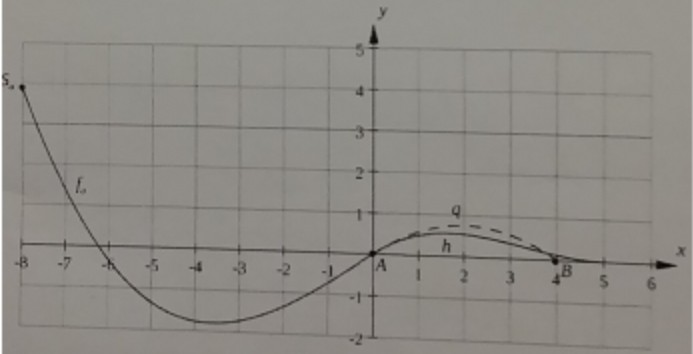
Die Sprungschanzen werden ausgehend vom Startpunkt \( S_{a}\left(-8 \mid f_{a}(-8)\right) \) von links nach rechts durchfahren und so eingebaut, dass der Absprungpunkt \( A(0 \mid 0) \) auf dem Niveau des Erdbodens liegt, das in der Seitenansicht durch die \( x \)-Achse festgelegt ist.
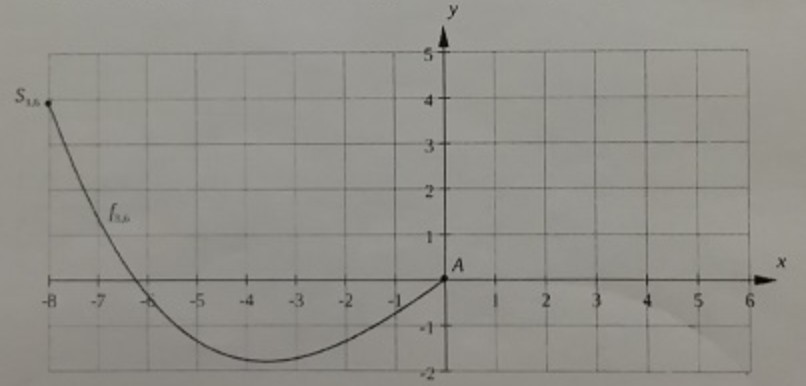
Der Funktionsgraph der Beispielfunktion \( f_{3,6} \) ist in der Abbildung dargestellt.
Zur Kontrolle: \( \left.T_{a}\left(-a \mid-\frac{1}{2} a\right)\right. \)
(3) Geben Sie eine Gleichung der Funktion k an, auf deren Graph alle Tiefpunkte \( T_{a} \) der Funktionsgraphen von \( f_{a} \) liegen.
(1) Zeigen Sie, dass alle Sprungschanzen, deren Profil durch eine der Funktionen \( f_{2} \) gegeben ist, im Absprungpunkt A dieselbe Steigung haben.
(3) Rechts vom Punkt \( A \) soll ein Aufsprunghügel angelegt werden, dessen seitliches Profil durch den Graphen der Funktion \( \mathrm{h} \) mit der Gleichung \( h(x)=\frac{3}{100} x^{3}-\frac{3}{10} x^{2}+\frac{3}{4} x, 0 \leq x \leq 5 \), beschrieben wird (siehe Abbildung 2). Berechnen Sie die Koordinoten des Punktes \( C \), in dem der BMX-Fahrer aus (2) den größten vertikalen Abstand vom geplanten Aufsprunghügel hätte.