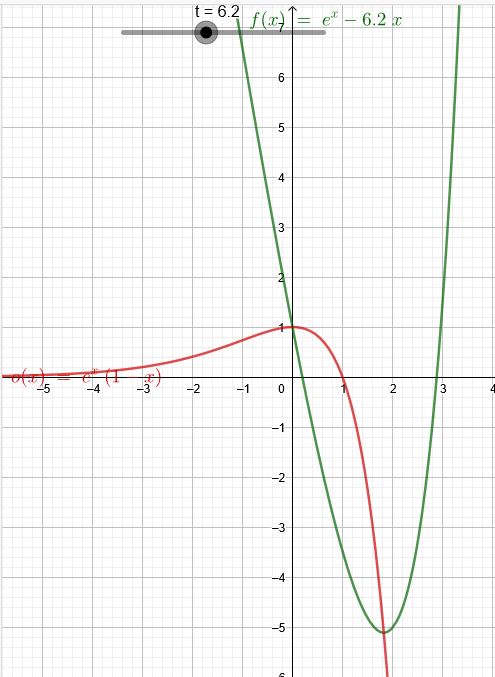
Auf welcher Ortskurve liegen die Tiefpunkte der Graphen von \(f_t\) ?
\(f_t(x) = e^x-tx \)
\(f_t(ln(t)) = e^{ln(t)}-t \cdot(t) \)
\(f_t(ln(t)) =t - t \cdot ln(t) \)
\(x=ln(t)\) \(y=t - t \cdot ln(t)\)
Die x-Koordinate nach t auflösen
\(x=ln(t)\) \(t=e^x\) Dies nun in \(y=t - t \cdot ln(t)\) einsetzen:
\(y=e^x - e^x \cdot ln(e^x)\)
Ortskurve: \(o(x)=e^x - e^x \cdot x=e^x(1-x)\)
Es fällt auf, dass \(f_t(x) = e^x-tx \) bei allen Werten von \(t\) durch das Maximum der Ortskurve läuft.